Математическое моделирование течений вязкой жидкости
ВВЕДЕНИЕ
В конце XIX столетия наука о движении жидкости распалась на две ветви, почти не связанные между собой. С одной стороны, достигла большого совершенства теоретическая гидродинамика, исходившая из уравнений Эйлера для движения идеальной жидкости. Однако результаты этой так называемой классической гидромеханики во многом резко противоречили опыту. Особенно резкое противоречие получалось в весьма важных вопросах о потере давления в трубах и каналах и о сопротивлении, которое оказывает жидкость движущемуся в ней телу; поэтому классическая гидромеханика имела для практики лишь небольшое значение, что и побудило создать для решения важных проблем, выдвигавшихся быстро развивавшейся техникой, свою собственную науку о движении жидкости, так называемую гидравлику. Эта наука, принявшая резко выраженный эмпирический характер, опиралась на большое число экспериментальных результатов и очень сильно отличалась от теоретической гидродинамики как своими методами, так и своей целью.
В начале настоящего столетия Л.Прандтль нашел путь, позволивший вновь соединить в одно целое указанные выше далеко отошедшие друг от друга ветви науки о движении жидкости. Кроме того, связав теорию с практикой, Л.Прандтль положил начало направлению, дальнейшее развитие которого в современной гидродинамике привело на протяжении первой половины настоящего столетия к неожиданным успехам. В этом состоит большая заслуга Л.Прандтля. Правда, уже давно было известно, что резкое расхождение между результатами классической гидродинамики и действительностью возникало в очень многих случаях вследствие пренебрежения в теоретических исследованиях вязкостью жидкости. Тогда же были составлены уравнения движения жидкости с учетом трения, так называемые уравнения Навье - Стокса для движения вязкой жидкости. Однако эти уравнения вследствие больших математических трудностей не удалось применить к теоретическому исследованию движений жидкости с трением (за исключением немногих частных случаев).
Между тем для воды и воздуха, т.е. для жидкостей, особенно важных в технике, коэффициент вязкости весьма мал, и, следовательно, силы трения, обусловленные вязкостью, получаются в целом очень небольшими по сравнению с остальными силами (силою тяжести и силами давления); поэтому долгое время не удавалось понять, каким образом малые силы трения, которые в классической теории считалось возможным отбрасывать, оказывали тем не менее решающее влияние на процесс движения.
В 1904 г. Л. Прандтль в своем докладе "О движении жидкости при очень малом трении", прочитанном на математическом конгрессе, указал путь, сделавший доступными теоретические, исследования течений жидкости с трением в практически важных случаях. А именно, исходя из теоретических соображений и некоторых простых экспериментов, Л. Прандтль показал, что течение в окрестности тела можно разделить на две области: на область очень тонкого слоя вблизи тела (пограничный слой), где трение играет существенно роль, и на область вне этого слоя, где трением можно пренебрегать. Эта гипотеза, с одной стороны, позволила получить физически очень наглядное объяснение важной роли вязкости в проблеме сопротивления, а с другой стороны, дала возможность преодолеть математические трудности и тем самым открыла путь теоретическому исследованию течений жидкости с трением. Свои теоретические соображения Л. Прандтль уже тогда подтвердил некоторыми очень простыми опытами в небольшом, построенном им самим, гидроканале. Таким образом, гипотеза Л. Прандтля положила начало восстановлению утраченной связи между теорией и практикой. Теория пограничного слоя Прандтля оказалась чрезвычайно плодотворной и сразу же после своего опубликования дала мощный толчок к дальнейшему развитию теоретических исследований[1]. Под влиянием задач, поставленных в нашем столетии расцветом авиационной и космической техники, новая теория весьма быстро развивалась и вскоре превратилась, вместе с другими важными теориями - теорией крыла и теорией движения газа при больших скоростях, - в основу современной механики жидкости и газа.
Существенный успех в этой области, был достигнут только после введения Л. Прандтлем понятия пути перемешивания. Введение этого понятия наряду с выполнением систематических опытов позволило применить теорию пограничного слоя для теоретического исследования турбулентных течений. В дальнейшем, под влиянием сильного возрастания скоростей в аэрокосмической технике, были тщательно исследованы пограничные слои для движений сжимаемой среды. При таких движениях, наряду с динамическим пограничным слоем, образуется температурный пограничный слой, играющий большую роль в теплопередаче между текущей средой и обтекаемым телом. При больших числах Маха тепло, выделяющееся вследствие трения между движущимся телом и средой, приводит к сильному нагреванию поверхности обтекаемого тела. Расчет этого нагревания представляет собой трудную проблему, особенно для ракет и искусственных спутников ("тепловой барьер").
Все реальные жидкости обладают вязкостью и поэтому их называют вязкими. В некоторых задачах влиянием вязкости можно пренебречь и ввести понятие - идеальная жидкость, вязкость которой равна нулю[2]. Для всех реальных жидкостей и газов такие физические характеристики, как вязкость, теплоемкость, теплопроводность и т.д. зависят от их параметров, например, от температуры. Но во многих задачах с достаточной степенью точности можно полагать эти величины постоянными.
Идеальная жидкость - это жидкость, не обладающая трением. При движении жидкости без трения между отдельными ее соприкасающимися слоями возникают только нормальные силы (давления), касательные же силы (напряжения сдвига) отсутствуют. Это означает, что идеальная жидкость не оказывает изменению формы никакого внутреннего сопротивления.
Теория движения идеальной жидкости математически очень глубоко разработана и во многих случаях дает вполне удовлетворительную картину действительных движений. В то же время теория идеальной жидкости совершенно бессильна для решения проблемы изучения сопротивления тела, движущегося в жидкости, так как в этом случае она приводит к результату, что тело, равномерно движущееся в неограниченно распространенной жидкости, не испытывает никакого сопротивления (парадокс Даламбера).
Такой совершенно неприемлемый результат тео рии идеальной жидкости объясняется тем, что в действительных жидкостях между жидкостью и поверхностью обтекаемого тела действуют не только нормальные, но и касательные силы. Эти касательные силы, или, другими словами, силы трения действительных жидкостей, связаны как раз с тем свойством жидкости, которое и называется вязкостью.
В идеальной жидкости касательные силы отсутствуют, поэтому на поверхности соприкосновения твердого тела с жидкостью в общем случае имеется разность касательных скоростей, т.е. происходит скольжение жидкости вдоль стенки. Напротив, в действительной жидкости на обтекаемую твердую стенку передаются касательные силы (силы трения), и это приводит к тому, что жидкость прилипает к стенке.
Наличие касательных напряжений (напряжений сдвига) и прилипание жидкости к твердым стенкам существенно отличают действительную жидкость от идеальной. Некоторые жидкости, важные в практическом отношении, например, вода и, особенно, воздух, обладают малой вязкостью. Течения таких маловязких жидкостей во многих случаях хорошо совпадают с течениями идеальной жидкости, так как касательные силы в них в общем являются очень малыми. Поэтому в теории идеальной жидкости вязкость совершенно не учитывают, поскольку это проводит к существенному упрощению уравнений движения, что позволяет построить широкую математическую теорию. Необходимо, однако, подчеркнуть, что в жидкостях даже с очень малой вязкостью, в противоположность идеальной жидкости, прилипание к стенкам все же существует, что является физической причиной указанного выше несоответствия между законами сопротивления для действительной и идеальной жидкостей (парадокс Даламбера).
Сущность вязкости жидкости можно уяснить на опыте Куэтта. Рассмотрим течение между двумя очень длинными параллельными плоскими пластинами, из которых одна, например, нижняя, неподвижна, в то время как другая движется в собственной плоскости с постоянной скоростьюu (см.
рис 1). Обозначим расстояние между пластинами через h
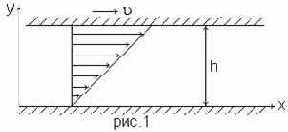
и предположим, что давление во всем пространстве, занимаемом жидкостью, постоянно. Опыт показывает, что жидкость прилипает к обеим пластинам, следовательно, непосредственно около нижней пластины скорость жидкости равна нулю, а непосредственно около верхней пластины она совпадает со скоростью u верхней пластины. Далее, опыт показывает, что в пространстве между пластинами имеет место линейное распределение скоростей, т.е. скорость пропорциональна расстоянию "у" от нижней пластины и выражается формулой

Для того, чтобы существовало такое состояние движения, к жидкости со стороны верхней пластины должна быть приложена касательная сила в направлении движения, уравновешивающая силы трения жидкости. На основании результатов опыта эта сила (отнесенная к единице площади пластины) пропорциональна скорости u верхней пластины и обратно пропорциональна расстоянию h между пластинами. Следовательно, сила трения t, отнесенная к единице площади, т.е. касательное напряжение, пропорционально отношению u/h, вместо которого можно взять отношение du/dy. Множитель пропорциональности между t и du/dy , обозначенный через m, зависит от природы жидкости. Он мал для так называемых маловязких жидкостей, например, для воды и спирта, и, напротив, велик для очень вязких жидкостей, например, для масла и глицерина. Таким образом, имеем элементарный закон трения жидкости в следующем виде:

Величина m[Па×с] называется динамическим коэффициентом вязкости и представляет собой физическую характеристику жидкости. Закон трения, выражаемый вышеприведенным равенством, называют законом Ньютона.
Необходимо подчеркнуть, что рассмотренное нами движение представляет очень простой, частный случай. Течение, изображенное на рис.1, называется движением чистого сдвига.
Во многих движениях жидкости, где наряду с силами вязкости действуют также силы инерции, важную роль играет отношение вязкости m к плотности r, называемое кинематическим коэффициентом вязкости

Необходимо отметить, что динамическая вязкость сильно зависит от температуры, причем для жидкостей при повышении температуры она уменьшается, а для газов - возрастает. Давление мало влияет на значения m.
1. ЛАМИНАРНОЕ ТЕЧЕНИЕ ВЯЗКОЙ ЖИДКОСТИ
1.1. Понятие о пограничном слое
Под пограничном слоем понимают тонкую при известных условиях в поперечном направлении к потоку область течения, где, в отличие от окружающего ее безвихревого потока, движение является вихревым и характеризуется сосредоточенными в этой области резкими изменениями скорости (скоростной пограничный слой), температуры (температурный пограничный слой), концентрации примеси (концентрационный или диффузионный пограничный слой). Скоростным (или динамическим) пограничным слоем называют тонкий слой жидкости, прилегающий к поверхности обтекаемого тела и заторможенный вследствие трения. Температурным (или тепловым) пограничным слоем называется примыкающая к поверхности тела область течения, в которой температура жидкости изменяется от ее значения на стенке до значения температуры внешнего потока жидкости. При этом температура стенки и температура жидкости у стенки принимаются равными друг другу. Диффузионным пограничным слоем называется область течения вблизи стенки, в которой происходит изменение концентрации примеси от ее значения на стенке до значения во внешнем потоке.
Различают ламинарные
и турбулентные пограничные слои в зависимости от ламинарного или турбулентного режима течения в них. Основным условием образования скоростных ламинарных погранслоев является малая вязкость жидкости, или точнее, большое значение числа Рейнольдса

(u - скорость потока; l - характерный размер), не достигающее, однако, той критической величины, при которой режим течения в пограничном слое становится турбулентным. Аналогично для температурных слоев подобным условием становится достижение больших значений числа Пекле Ре=Pr×Re (число Прандтля

Физическая картина образования пограничных слоев на твердых поверхностях состоит в следующем. Однородный безвихревой поток, достигнув поверхности твердого тела, "прилипает" к нему частицами, непосредственно соприкасающимися с поверхностью тела, в то время как соседние слои продолжают двигаться с резко увеличивающимися по мере удаления от поверхности скоростями, что приводит к завихренности потока. Образовавшиеся вблизи поверхности вихри, с одной стороны, сносятся набегающим потоком, участвуя в конвекции, а с другой - диффундируют в жидкость, окружающую тело. Если конвекция велика по сравнению с диффузией (что соответствует большим числам Рейнольдса), на поверхности сохраняется весьма тонкий слой заметно завихренной жидкости - так называемый пристенный пограничный слой.
Имея некоторую начальную завихренность, возникшую при выходе из сопла или сходе с поверхности обтекаемого тела, аналогично образуются "свободные" пограничные слои: "затопленные струи" и "следы" за кормой тела.
Под толщиной пограничного слоя d подразумевают расстояние от поверхности обтекаемого тела до такой точки в потоке (у=d), где практически с заданной степенью приближения можно принять продольную скорость в пограничном слое равной ее значению в той же точке внешнего безвихревого потока. Геометрическое место таких точек дает приближенное представление о внешней границе пограничного слоя.
Необходимо отметить, что безразмерная толщина пограничного слоя




( в соответствии с выражением




(где знак ~ означает порядок величины).
В результате получаем первое основное свойство ламинарного пограничного слоя:


Полученное равенство выражает общий для всех плоских, стационарных ламинарных пограничных слоев закон изменения их относительных толщин обратно пропорционально корню квадратному из рейнольдсова числа потока.
Опыт показывает, что в потоках вязких жидкостей или газов около поверхности твердого тела действие сил вязкости в разных областях течения проявляется неодинаково. Оно проявляется заметно там, где возникают большие поперечные градиенты скорости и, как следствие, касательные напряжения велики. По мере увеличения расстояния от стенки действие сил вязкости ослабевает и становится малым на сравнительно небольшом удалении. В обычных условиях течения скорость частиц жидкости u относительно обтекаемой поверхности на самой поверхности равна нулю. (Необходимо заметить, что область течения, в которой газ можно рассматривать как сплошную среду, прилипающую к обтекаемой поверхности, характеризуют условием

Уравнения Стокса движения реальной, вязкой несжимаемой жидкости отличаются от уравнений Эйлера движения идеальной жидкости наличием члена

С математичес кой стороны, этот член меняет общий характер дифференциальных уравнений движения, повышает их порядок. Кроме того, что особенно существенно, к граничному условию непроницаемости твердых стенок (нормальная скорость относительно стенки равна нулю) прибавляется новое граничное условие - отсутствие скольжения жидкости на стенке (составляющая скорости в касательной плоскости к стенке равна нулю). Можно показать, что уравнения Эйлера вообще не имеют решений, удовлетворяющих последнему граничному условию, однако опыты показывают, что распределение давлений по поверхности хорошо обтекаемого крылового профиля и картина линий тока вокруг него мало отличаются от теоретически рассчитанных по формулам безвихревого обтекания идеальной жидкостью. Этот важный экспериментальный факт объясняется тем, что при сравнительно больших числах Re, характерных для практических (в авиации, кораблестроении, турбостроении и т.д.) обтеканий тел, область потока, в которой проявляется влияние вязкости, сводится к весьма тонкому по сравнению с размерами обтекаемого тела пограничному слою, расположенному непосредственно вблизи поверхности тела и распространяющемуся вниз по потоку за телом в виде так называемого аэродинамического следа (рис. 2).
Вне тонкого, постепенно увеличивающегося по толщине вниз по потоку пограничного слоя реальная жидкость ведет себя как идеальная;
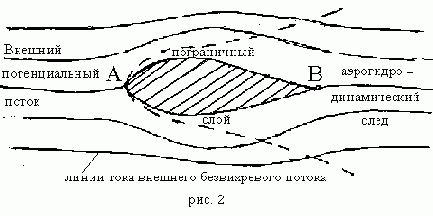
характер движения в ней (слабая по сравнению с пограничным слоем и аэродинамическим следом завихренность) не может привести к сколько-нибудь значительным проявлениям сил вязкости. Наоборот, в пограничном слое, где касательные к стенке составляющие скорости резко меняются от нуля до величины порядка скорости набегающего потока, за счет больших величин производных от скорости по нормами к поверхности тела возникают значительные силы вязкости (

Принимая жидкость вне пограничного слоя и аэродинамического следа за идеальную, можно считать движение в этой области безвихревым, потенциальным. Только пройдя сквозь область пограничного слоя на поверхности обтекаемого тела, поток становится вихревым и затем, уже оставив тело и попав в область аэродинамического следа, постепенно теряет полученную завихренность, исчезающую вследствие диффузии, причем энергия вихрей превращается в тепло, рассеивающееся благодаря теплопроводности.
Как показывают непосредственные измерения, пограничный слой при тех больших значениях чисел Re, с которыми приходится иметь дело на практике, очень тонок. Возрастая по толщине от носка крыла к его хвосту, пограничный слой даже в точке максимальной толщины слоя вблизи хвоста крыла, достигает обычно лишь порядка сотых частей хорды. Так, на крыле самолета с хордой 1,5-2 м пограничный слой на режиме максимальной скорости имеет порядок нескольких сантиметров, а на корабле, длина которого имеет порядок 100 м, может достигать толщины 1 м. Такой тонкий сравнительно с размерами тела слой не может произвести значительных возмущений во внешнем по отношению к нему безвихревом потоке, чем и объясняется совпадение картин обтекания тел реальной и идеальной жидкостью. Важно отметить, что характерная для движения вязкой жидкости в тонких слоях неизменность давления в поперечном к потоку направлении приводит к тому, что давление на внешней границе пограничного слоя передается сквозь пограничный слой без изменений на поверхность обтекаемого тела.
В приведенном рассуждении терминам границы и толщины пограничного слоя не придается точного количественного смысла. Эти понятия лишь качественно характеризуют поперечный размер области, где скорости от нулевого значения на стенке изменяются до величины порядка скоростей внешнего потока. Так, например, под толщиной погранслоя можно подразумевать такое расстояние от стенки, на котором скорость будет отличаться от скорости внешнего потока на 1%.
Введем в рассмотрение так называемые интегральные толщины пограничного слоя:
 |
толщина вытеснения масс в пограничном слое, учитывающая смещение линий тока из-за наличия вязкости (торможение жидкости в пограничном слое [4]); |
 |
толщина потери импульса, учитывающая потерю количества движения на преодоление трения. |

Введем интегральные толщины:

Разделив обе части последнего уравнения на


Дифференцируя первый член левой части уравнения (1.25), получим:

или окончательно:

Это интегральное соотношение или уравнение импульсов впервые было выведено учеником Прандтля -Кáрманом и носит название интегрального соотношения Кармана.
В выводе этого соотношения есть одна некорректность, т.к. используем уравнение Эйлера




Тогда интегральные толщины пограничного слоя будут таковы:


и граничные условия следующие;
1) граничное условие на стенке: у=0; uх=0 (как и было ранее)

2) на внешней границе пограничного слоя у=d; uх=uх,¥=u¥;

Необходимо отметить, что если для ламинарного пограничного слоя метод интегрального соотношения не является единственным, то для турбулентного погранслоя этот метод является единственным методом решения задачи.
В общем случае все задачи о ламинарном пограничном слое могут решаться двумя путями. В первом случае решают дифференциальные уравнения погранслоя с соответствующими граничными условиями и обычно получают значение скоростей во всей области пограничного слоя, т.е. uх(х,у) и uу(х,у), а следовательно, и трение на стенке. Такой способ называется точным методом решения задачи о ламинарном погранслое. Во втором случае пользуются не дифференциальными уравнениями, а интегральными соотношениями.
При этом задаются некоторой формой профиля скоростей в пограничном слое и, используя интегральное соотношение Кармана, определяют напряжение трения tw на обтекаемой поверхности, а также такие интегральные величины, как толщина пограничного слоя d, толщина вытеснения d* и толщина потери импульса d**. Такой способ решения называют приближенным методом.
В качестве примера рассмотрим приближенную математическую модель продольного обтекания вязкой жидкостью плоской бесконечно тонкой пластины. Очевидно, в этом случае давление во всей области потока, как и величина скорости вне пограничного слоя, будут величинами постоянными.
Граничные условия будут следующие:
а) при у=0 uх=uу=0.
Если рассмотреть первое дифференциальное уравнение пограничного слоя (1.20) - уравнение движения

то, т.к. для бесконечно тонкой плоской пластины


Таким образом, при у ® 0

б) при у=d uх=u¥;


Уравнение импульсов (или интегральное соотношение Кáрмана) для этой задачи имеет вид:

т.к.

Идея интегрального соотношения состоит в задании неизвестного поля скоростей простейшим полиномом:

Значения коэффициентов а0, а1, а2,... могут быть найдены из граничных условий, причем для определения одного коэффициента полинома требуется одно граничное условие. Таким образом, количество членов полинома должно соответствовать количеству поставленных граничных условий.
Воспользуемся для начала тремя граничными условиями:
а) на стенке при у=0 ® uх=0,
б) на границе слоя при у=d ® uх=u¥ ;

Подставив эти граничные условия в полином, в котором берем три первых члена

1) при у=0,

2) при

3) при

Из последних двух уравнений:

находим


Следовательно, поле скоростей будет иметь вид:


Зная





Отсюда видно, что d>d*>d**, т.е. толщина пограничного слоя больше толщины вытеснения, а та, в свою очередь, больше толщины потери импульса.
Из полученных значений d* и d** определим:


Величина напряжения трения на стенке определяется формулой:

Найдем





Тогда уравнение импульсов


или




Считая, что при х=0 ® d=0, получим С1=0.
Окончательно будем иметь:


где

Из формулы





Зная выражение для толщины пограничного слоя d, можно найти зависимость для напряжения трения на стенке:

Таким образом,


Полное сопротивление (в данном случае полное сопротивление трения) можно определить для одной стороны пластины по формуле:

где b - ширина пластины, l - длина пластины.
Если принять ширину пластины b=1, то Rx для одной стороны пластины будет


Для пластины в целом величина трения будет определяться удвоенной величиной (две стороны пластины), т.е.

или

При b=1

Коэффициент сопротивления трения равен:

где S=2b×l - площадь поверхности с двух сторон пластины.
При b=1 ®

где

Как видно,


Еще раз напоминаем, что этот метод для ламинарного погранслоя был открыт Карманом и разработан далее Рэлеем. В действительности, скорости течения на практике так велики, что ламинарное движение переходит в турбулентное, где метод интегральных соотношений является единственным, позволяющим получить конечные результаты.
1.5 Математическое моделирование обтекания ламинарным потоком профиля произвольной формы
Существующие методы приближенного решения задачи о ламинарном пограничном слое на профиле произвольной формы основаны на решении уравнения импульсов. Рассмотрим один из наиболее простых методов, предложенный Н.Е. Кочиным и Л.Г. Лойцянским. Так как в уравнение, импульсов ( 1.26) входят три неизвестных: d*, d** и

Выбрав такие профили, можно выразить d*, d** и

В качестве такого параметра можно ввести величину f (называемую формпараметром), которая определяется выражением:

Тогда семейство профилей скоростей в ламинарном пограничном слое будет выражаться зависимостью:

а параметры d*, d** и tw можно представить в виде:

где


Эта формула получается следующим образом:




Если обозначить через


Отсюда

Тогда


Умножив обе части этого уравнения на


Учитывая, что коэффициент при втором члене последнего уравнения равен


Обозначим:

Учитывая, что


Так как


Это дифференциальное уравнение формпараметра.
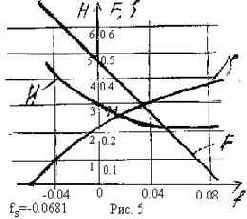
Зная F(f) , можно при заданном значении u¥ решить уравнение (1.31) и найти f(x), а следовательно, d** и tw. Из точных решений, подтвержденных экспериментом, было установлено, что F(f) можно приближенно представить в виде линейной функции:
F(f)=a-b×f.
 |

Это линейное дифференциальное уравнение первого порядка имеет следующее решение:

Если точка x=0 совпадает с передней критической точкой обтекаемого тела, в которой скорость внешнего потока u¥=0, то из условия конечности значения формпараметра f в этой точке получим с=0 и решение будет иметь окончательный вид:

Поскольку из этого решения нельзя определить значение формпараметра в точке, где u¥=0, то используют уравнение импульсов в виде:

В точке, где u¥=0, для конечности производной необходимо, чтобы F(f)=0. Но тогда из формулы F(f)=a-f×b следует, что в этой точке f|x=0=a/b. Для определения формпараметра f в начальной точке (x=0) можно поступить и следующим образом: из формулы

Раскроем неопределенность типа


Тогда

Таким образом, зная закон изменения скорости внешнего потока u¥(х), по выражению для f можно найти значение формпараметра для любого сечения пограничного слоя.
Выражая толщину d** потери импульса через формпараметр f, будем иметь


Так вычисляют все параметры ламинарного пограничного слоя.
Координаты точки отрыва S (как было показано ранее ) определяются из условия равенства нулю трения на стенке:


Тогда

здесь

Таким образом, в точке S отрыва пограничного слоя от профиляz(f) = 0. Из рис. 5 видно, что z(f) = 0 при значении формпараметра fs =-0.0681. Знак "-" свидетельствует о том, что отрыв происходит в области диффузора.
Необходимо обратить внимание, что функция u¥(х) определяется методами теории потенциальных течений в предположении, что пограничный слой отсутствует, и затем значения этой функции переносятся на его внешнюю границу. Это равносильно допущению, что ввиду малости толщины слоя он практически не изменяет потенциального потока, обтекающего данную. поверхность. Но в ряде случаев такое предположение оказывается недостаточно точным. Образование пограничного слоя приводит к изменению закона для скорости потенциального потока, т.е. имеет место обратное влияние пограничного слоя. Оно тогда должно учитываться в расчетах, особенно для течений в диффузорах, конфузорах, на начальных участках труб и каналов.
1.6 Математическое моделирование ламинарного течения
несжимаемой жидкости в трубах.
Рассмотрим установившийся ламинарный поток в круглой цилиндрической трубе, предположив линии тока прямыми, параллельными оси трубы (см.
рис. 6), Будем рассматривать стационарный процесс, для которого


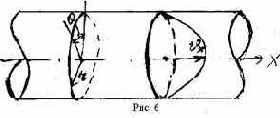
Предположим также, что среда несжимаема т.е. r=const. Кроме того, будем считать, что скорость потока и профиль скоростей не зависят от продольной координаты. Это так называемое стабилизированное движение, имеющее место в цилиндрической трубе на значительном расстоянии от входа. Следовательно, если направление движения совпадает с осью Х, то проекции скоростей на оси y и z будут равны нулю:

Используя уравнение неразрывности для несжимаемой жидкости:



Тогда уравнения движения Навье - Стокса вязкой несжимаемой жидкости, имеющие вид:
а) в векторной форме

б) в проекциях на оси декартовых координат:

после подстановки значений

ux=uz=0;




ux=u;

и отбрасывания внешних сил Fx =Fy =Fz =0 преобразуются к виду:

Из этих уравнений следует:
1) величина давления не зависит от поперечных координат y и z и есть функция только координаты x, т.е. в частности, в круглой трубе давление меняется только вдоль оси, а, следовательно, постоянно в каждом сечении и не зависит от радиуса r ;
2) так как левая часть первого уравнения зависит только от у и z, а правая часть не зависит ни от у, ни от z, то следовательно, правая и левая части этого уравнения должны быть равны одной и той же постоянной величине, т.е.

Таким образом, уравнение Навье - Стокса для стабилизированного движения жидкости в цилиндрической трубе вдоль оси X будет иметь вид:

Если прямоугольную систему координат заменить на цилиндрическую, в которой x=x, y=r*cos(q); z= r*sin(q), то уравнение (1.32) примет вид:

Предполагая, что поток в трубе обладает осевой симметрией, заключаем, что все параметры не зависят от переменной q, т.е.



Так как


Выполним последовательно двойное интегрирование.
После первого интегрирования получим:


Проинтегрируем еще раз:

Постоянные интегрирования С1 и С2 определяются из граничных условий. Для круглой трубы с радиусом R они могут быть записаны так: при r=R (внутренний радиус трубы) скорость u=0; при r=0 скорость u - конечная величина.
Так как скорость потока в трубе должна иметь конечное значение (или нулевое при r=R ), а при r® 0 формула (1.34) дает бесконечное значение скорости на оси, то физически реальный результат получим лишь при C1 = 0. Используя первое граничное условие, найдем:


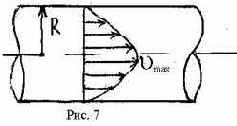
Таким образом, для круглой трубы имеем параболическое распределение скоростей по сечению (рис. 7).
 |

Тогда

или в безразмерном виде

Очевидно, что пространственная эпюра скоростей представляет собой параболоид вращения с основанием pR2 и высотой umax. Для цилиндрической трубы можно записать

где Dp - перепад давления в трубе длиной l.
Определим среднюю расходную и максимальную скорости в круглой трубе. Объемный расход жидкости равен:

Этот результат получается следующим образом:

Тогда

Поскольку расход Q связан со средней скоростью






Перепад давлений на участке трубы длиной l определяется как

где D - внутренний диаметр трубы.
Это формула Пуазейля, исследовавшего законы движения крови по капиллярным сосудам.
С другой стороны, для установившегося движения в цилиндрических трубах перепад давления определяется по формуле Дарси - Вейсбаха:

Приравнивая оба равенства, получим:


где


Выражение коэффициента сопротивления l как функции числа Рейнольдса (

Необходимо отметить, что полученные соотношения пригодны для ламинарного течения только лишь на определенном расстоянии от входа в трубу, после исчезновения начального участка ламинарного потока (см. рис. 8).
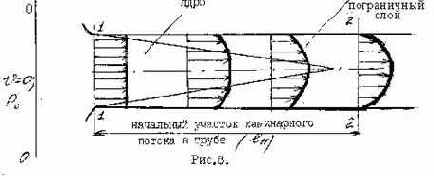
Если вход в трубу из резервуара выполнен достаточно плавно, то в начальном сечении 1-1 устанавливается практически равномерное распределение скоростей. По мере движения жидкости тормозящее влияние стенок распространяется на всё большую толщу потока. На некотором участке, называемым начальным, поток имеет ядро, где сохраняется равномерное распределение скоростей, и пристенный пограничный слой, где скорости распределяются неравномерно. Сечение ядра вниз по течению убывает, а толщина пограничного слоя возрастает. В конце начального участка lн пограничный слой смыкается на оси трубы, и ниже по течению устанавливается параболическое распределение скоростей в соответствии с полученными соотношениями.
Этот характер течения и соответствующие ему зависимости имеют место только при устойчивом ламинарном режиме, т.е. при Re< Reкр. При Re, немного меньших Reкр, в ламинарном потоке периодически появляются кратковременные очаги турбулентности, которые могут на отдельных участках заполнять все сечение потока, образуя "турбулентные пробки".
При возрастании числа Re, турбулентный режим в каждом сечении существует все более длительное время и, наконец, поток становится турбулентным. Появление турбулентных очагов наступает тем раньше, чем больше возмущений испытывает поток при входе в трубу. Если вход сделать плавным и устранить другие источники возмущений, то ламинарный режим можно получить и при больших числах Re (например 20.000). Однако такие "затянутые" ламинарные режимы оказывались неустойчивыми, т.е. внесение в поток даже очень малых возмущений приводило к турбулизации. Поэтому критические значения числа Re следует понимать как границу устойчивого ламинарного режима в том смысле, что при. Re < Reкр любые внешние возмущения, вносимые в поток, будут с течением времени затухать и поток сохранит ламинарный характер.
При Re > Reкр в зависимости от условий опыта может существовать ламинарный или турбулентный режим. Для круглых труб Reкр = 2300. Такое определение Reкр соответствует так называемому нижнему критическому числу Re. Верхним критическим числом Re называют то его значение, при котором устанавливается стабильный турбулентный режим.
2. МАТЕМАТИЧЕСОКЕ МОДЕЛИРОВАНИЕ ТУРБУЛЕНТНЫХ ТЕЧЕНИЙ
ВЯЗКОЙ ЖИДКОСТИ
2.1. Переход ламинарного течения в турбулентное
Исторически первыми научными наблюдениями турбулентного движения были опыты английского физика 0. Рейнольдса, в которых он в 1893 году изучал движение воды в круглой цилиндрической трубе [5]. При повышении скорости ламинарно движущейся жидкости было замечено, как на подкрашенную и хорошо видимую вначале прямолинейную струйку начинают накладываться волны, распространение которых вдоль струйки говорит о появлении возмущений в ранее спокойном прямолинейном движении. Постепенно с ростом скорости воды число таких волн и их амплитуда возрастает, пока, наконец, струйка не разобьется на нерегулярные, перемешивающиеся между собой более мелкие струйки, хаотический характер которых позволяет судить о переходе ламинарного движения в турбулентное. Таким образом, с возрастанием скорости ламинарное движение теряет свою устойчивость, при этом случайные возмущения, которые вначале вызывали лишь колебания струек относительно устойчивого их прямолинейного положения, быстро развиваются и приводят к новой форме движения жидкости - турбулентному движению.
Если местная скорость


Неупорядоченное движение частиц в турбулентном потоке создает резкие изменения местных скоростей во времени, называемые пульсациями скорости.
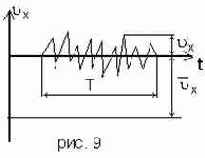 |

где uх - мгновенная местная скорость, Т - период осреднения. Такой способ осреднения не является единственным, но благодаря простоте его широко применяют в гидромеханике. При этом можно предположить, что для каждого турбулентного движения существует такой достаточно большой по сравнению с периодом турбулентных пульсаций постоянный период осреднения Т, что сглаживание по времени приводит к осредненной величине, при повторном сглаживании уже не изменяющейся, т.е.





По правилу осреднения также следует, что среднее значение производной от скорости по координате равно производной от среднего значения скорости по той же координате, т.е.


Правила осреднения обладают еще и следующими свойствами [6]:




Величина


Равенство коэффициента корреляции R=±1 говорит о полной, детерминированной связи явлений, описываемых uх и uу (причем знак "-" говорит о противоположных фазах колебаний), а равенство R=0 говорит о статистической независимости явлений. Коэффициент корреляции между пульсациями, происходящими в двух разных точках пространства и, вообще говоря, в различные моменты времени, называется коэффициентом двухточечной пространственно - временной корреляции, причем, в зависимости от количества коррелируемых пульсирующих функций, двойной, тройной и т.д. корреляции.
Пульсационные составляющие скорости могут быть охарактеризованы частотой и амплитудой, которые при турбулентном движении изменяются в широких пределах. В каждой точке турбулентного потока имеют место пульсационные скорости с целым спектром частот: от низких (5-10Гц) до очень высоких(50-100кГц). Средняя амплитуда пульсаций скорости характеризуется величинами равными:





Интенсивность турбулентности изменяется от 0.3% в атмосфере до 7-8% и более в машинах.
В своих опытах Рейнольдс впервые обнаружил, что переход ламинарного движения в турбулентное обусловливается достижением критического значения некоторого безразмерного числа, или критерия, которое в дальнейшем получило его имя. По опытам самого, Рейнольдса критическое число оказалось равным

здесь uср - средняя по расходу скорость, d - диаметр трубы. Впоследствии им же было открыто существование нижнего критического значения Reкр » 2000, такого, что при Re < Reкр движение в трубе оставалось ламинарным, каковы бы ни были введенные в течение возмущения. Вместе с тем было замечено, что путем удаления возмущений на входе в трубу или уменьшения начальной их интенсивности можно искусственно затянуть ламинарное движение в область значительно бóльших значений числа Re, например, до 5×104.
Конечно, такое затянутое ламинарное движе ние не терпит появления даже очень небольших возмущений и сразу же переходит в турбулентное.
2.2. Турбулентный пограничный слой в несжимаемой жидкости
Явление перехода ламинарного движения в турбулентное в круглой цилиндрической трубе распространяется и на движение вязкой жидкости в пограничных слоях на поверхности твердых тел, в струях и в следах за телами. Если условиться количественно сопоставлять скорость на внешней границе пограничного слоя со скоростью на оси трубы, а толщину погранслоя с радиусом трубы, то можно ввести в рассмотрение число Red пограничного слоя:

Многочисленные опыты по определению критического числа для пограничного слоя на пластине привели к значениям, близким к критическому числу трубы. Тот же порядок Redкр был найден и при обтекании круглого цилиндра, шара и крыловых профилей. При этом было обнаружено, что относительное расположение критического сечения пограничного слоя, в котором ламинарный слой переходит в турбулентный, существенно зависит от степени возмущенности набегающего на тело внешнего потока. При изменении этого фактора изменяется и критическое число Рейнольдса пограничного слоя.
Наличие того или иного режима движения в пограничном слое обусловлено развитием течения вдоль пограничного слоя. Так, начальный участок слоя обычно бывает ламинарным, за ним располагается переходная область, где одновременно сосуществуют турбулентные зоны потока с ламинарными, и, наконец, область развитого турбулентного потока, состоящая из турбулентного ядра и тонкого вязкого ламинарного подслоя, граничащего с твердой стенкой.
Вместо Red можно рассматривать числа


По опытам на различных крыльях в разных аэродинамических трубах значение

Наблюдающиеся отличия в значениях


В случае свободного пограничного слоя, как, например, в струе или следе вдалеке за телом, критические числа Reкр очень малы, и практически всегда приходится иметь дело с турбулентными струями и следами за телом.
2.3. Математическая модель
осредненного турбулентного движения
Пусть имеем систему уравнений пограничного слоя:

Так как первый член в правой части первого уравнения системы (2.1) записан как



Для описания турбулентного движения Рейнольдс предложил следующий прием. Регистрируя во времени скорости и давления в данной точке потока, можно их представить как:

где



Под осредненным значением параметра понимается обычное интегральное среднее по времени t за промежуток T , называемый, периодом осреднения:



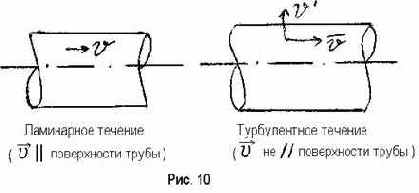
В турбулентном движении добавляется пульсационная составляющая скорости (рис.10), в результате чего наблюдается вихревое движение, при котором сопротивление значительно возрастает. Таким образом, турбулентное течение обладает бóльшим сопротивлением по сравнению с ламинарным движением.
Предложение Рейнольдса имеет физический смысл, поскольку турбулентное движение жидкости характеризуется непрерывными случайными пульсациями давления, компонент скорости и других гидродинамических величин. При этом каждая реализация турбулентного движения в одних и тех же условиях индивидуальна, т.е.
процесс является случайным (недетерминированным).
Поскольку все пульсирующие величины можно разложить на средние по ансамблю реализаций турбулентного течения - математические ожидания (обозначаемые черточками сверху), и собственно пульсации (обозначаемые штрихами), то и приходим к Рейнольдсову представлению случайного поля:

(Если ограничиться несжимаемой однородной жидкостью, то r=const и, следовательно,

Поле осредненных величин называется осредненным движением, а поле мгновенных значений - актуальным движением. Если осредненное движение не меняется со временем, поток называется установившимся или стационарным. В силу эргодического свойства стационарных случайных полей в установившемся потоке результат осреднения той или иной гидродинамической переменной по реализациям турбулентного движения совпадает с результатом осреднения по времени для любой одной реализации.
В настоящее время турбулентное движение принято характеризовать осредненным по времени значением величин. В уравнениях сохранения массы, количества движения и энергии в потоке вязкой жидкости истинные (мгновенные) величины заменяются осредненными во времени их значениями следующим образом. Истинные величины в данной точке турбулентного потока раскладываются на осредненные и пульсационные их значения, что соответствует физическому представлению турбулентного движения. Тогда уравнения неразрывности, движения и энергии для осредненного турбулентного движения несжимаемой жидкости в общем случае получаются из исходных уравнений после замены в них истинных значений переменных осредненными их значениями и пульсациями с последующим осреднением этих параметров по времени. При введении в действие новых переменных добавляется три неизвестных:

Рассмотрим решение задачи. Возьмем, например, уравнение:

Проведя операцию осреднения, его можно записать следующим образом:










Здесь а)



г)



где

Видно, что уравнения такие же, как и для ламинарного пограничного слоя, только с добавкой напряжений от турбулентных пульсаций


Для вывода уравнений турбулентного пограничного слоя надо осреднить исходные уравнения погранслоя, несколько преобразовав первое уравнение - уравнение движения (аналогично случаю ламинарного пограничного слоя).
Для этого уравнение неразрывности умножим на ux

и добавим его в левую часть первого уравнения системы (2.1)

В результате преобразований (как и в случае ламинарного погранслоя - уравнение (1.21)) первое уравнение системы (2.1) получим в виде:

Здесь:


Проведем над обеими частями этого равенства операцию осреднения:






Так как




Подставляя значения



Учитывая уравнение неразрывности в осредненном виде:

можно уравнение движения (2.4) записать так:

С этой целью левая часть уравнения (2.4) преобразовывается с учетом уравнения неразрывности следующим образом:

Уравнения (2.5) и (2.6) входят в систему дифференциальных уравнений Рейнольдса осредненного турбулентного движения несжимаемой вязкой жидкости, которую можно окончательно представить в виде:

Эта система имеет одинаковый вид как для основного течения жидкости, так и для течения жидкости в погранслое.
Сопоставим первое уравнение системы (2.7) с уравнением движения вязкой жидкости в напряжениях, которое выглядит следующим образом:

В случае одномерного стационарного движения и отсутствия массовых сил это уравнение имеет вид:

Сравнивая уравнение Рейнольдса с уравнением движения в напряжениях, можно представить себе правую часть уравнения Рейнольдса как результат подстановки в уравнение в напряжениях вместо величин pxx и pxy суммы вязких напряжений, определяемых обобщенным законом Ньютона, и дополнительных турбулентных напряжений p'xx и p'xy, возникших за счет наличия в потоке пульсаций, т.е.:


В нашем случае
а)




б)




Таким образом получаем полную тождественность уравнений движения в напряжениях (2.8) и Рейнольдса (2.7).
В общем случае трехмерного движения эти дополнительные турбулентные напряжения p'xx, p'xy и т.д. образуют, так же как и вязкие напряжения, симметричный тензор второго ранга:

называемый тензором турбулентных напряжений с компонентами

Итак, приходим к выводу: уравнения осредненного турбулентного движения могут быть написаны в той же форме, что и уравнения действительного движения, если только, помимо вязких (ньютоновских) напряжений, учесть еще дополнительные турбулентные напряжения.
Назовем тензором полного (суммарного) напряжения тензор P, равный

и имеющий компоненты:

Не только вид уравнений движения, но и вид уравнений импульсов (интегральное соотношение Кармана) в турбулентном пограничном слое остается таким же, как и для ламинарного пограничного слоя:

только значения d, d*, d** и tw (напряжение трения на твердой стенке) будут иными:
а) толщина вытеснения масс в пограничном турбулентном слое

б) толщина потери импульса в турбулентном погранслое

в) напряжение трения на твердой стенке

Граничные условия будут следующими :
а) на стенке:

б) на внешней границе турбулентного погранслоя:

Необходимо учесть, что уравнение Эйлера



2.4. Двухслойная схема пристенной турбулентности
Чтобы подчеркнуть главную особенность турбулентного движения около твердой стенки, рассмотрим установившееся движение жидкости вдоль безграничной пластины ['7]. Расположим ось координат так, чтобы ось х была направлена вдоль пластины, а ось у - по нормали к ней (рис. 11). При такой идеализации течения, когда поток совершает плоское стационарное осредненное движение при отсутствии массовых сил, любые два сечения, перпендикулярные линиям тока, идентичны в кинематическом и динамическом смысле. Это позволяет полагать все производные по X равными нулю, компоненты скорости



Сравним между собой ламинарное и осредненное турбулентное движения такого типа.
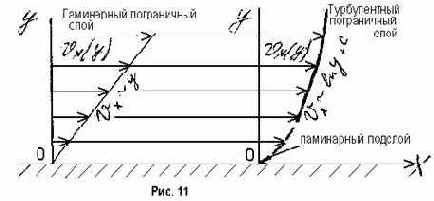
Замечая, что ux=ux(y); uy=uz=0; p=p(y), получим уравнения Навье -Стокса ламинарного движения в виде:
а)

б)

Проинтегрируем эти уравнения, преобразовав (2.17) к виду:
а)


б) р=const.
После повторного интегрирования уравнения (2.17) распределение скоростей ux(y) в ламинарном потоке будет:

При y=0 ux=0, т.е. на стенке скорость обращается в нуль, что дает постоянную интегрирования С2=0.
Тогда получаем следующее распределение скоростей ux(y) в ламинарном потоке:

Это свидетельствует о линейном профиле скоростей в ламинарном потоке и о постоянстве напряжения трения между любыми слоями в осредненном движении, равного напряжению трения на стенке:

Перейдем теперь к турбулентному движению, описываемому в нашем случае уравнением Рейнольдса.
Будет считать, что для безграничной пластины все параметры потока не зависят от х. Отбросив черточки над осредненными величинами скоростей (поскольку рассматривается осредненное движение), получим уравнение Рейнольдса осредненного движения несжимаемой вязкой жидкости.
В исходном виде уравнение Рейнольдса движения несжимаемой вязкой жидкости имеет вид:

Так как все производные по Х равны нулю (поскольку все параметры потока не зависят от Х); uy=0 для тонкой пластины, то, опуская черточки над uх, получаем:

или

где

После интегрирования получим:

Для определения постоянной интегрирования воспользуемся граничными условиями на стенке, т.е. при у=0. На стенке напряжение турбулентного трения


и, следовательно, получаем:

Рассмотрим отдельно каждое слагаемое. Напряжение вязкого трения

В целях изучения профиля скоростей в области преобладания турбулентных напряжений трения рассмотрим область, в которой


По аналогии с вязким трением турбулентное напряжение можно представить в виде:

где А и

В то время как коэффициенты молекулярного переноса (m и n) однозначно определяются физическими свойствами жидкостей и газов и их состоянием (температурой и давлением), но не зависят от динамических свойств потоков, коэффициенты турбулентного переноса определяются прежде всего статистическими свойствами движения.
Чтобы вывести формулу для турбулентного напряжения трения, Прандтль использовал некоторые физические предпосылки и теорию размерностей. Можно считать, что по аналогии с вязким трением величина турбулентного трения зависит от градиента скорости


где l - длина перемешивания, характеризующая собой масштаб турбулентности (т.е. средний размер связанных объемов жидкостей, участвующих в турбулентном переносе).
Замечая, что расстояние "у'' данной точки от твердой стенки представляет собой единственную характерную для этой точки в безграничном потоке длину, Прандтль предложил наиболее простую зависимость
l=æ×у,
где æ - коэффициент пропорциональности (числовая константа, определяемая из опыта). Необходимо отметить, что эта формула имеет место лишь в пристеночной области. Подставив эту зависимость в формулу ( 2.24), получим:

Решая это уравнение относительно


Этот так называемый логарифмический профиль скоростей в турбулентном потоке существенно отличается от ламинарного линейного распределения скоростей вблизи стенки.
Так как последняя формула была выведена в предположении, что исследуется движение на некотором расстоянии от стенки, то она может и не удовлетворяться при у=0 и, следовательно, нельзя находить произвольную постоянную "С"- из граничных условий на стенке. Действительно, при у = 0 скорость


Поэтому для определения постоянной интегрирования "С" приходится выделять вблизи твердой границы тонкий "вязкий подслой" с линейным профилем скоростей, а затем произвести сращивание логарифмического решения с линейным.
Согласно прежним рассуждениям, будем искать такое расстояние от стенки у=dл, для которого при у<dл существенно преобладает вязкое трение, а при у>dл - турбулентное трение, т.е. при у<dл движение будет ламинарным, а при у>dл - турбулентным. Величина dл называется толщиной ламинарного вязкого подслоя. В действительности такой резкой границы между пристеночным подслоем ламинарного движения и областью турбулентного движения не существует. С физической точки зрения весь поток можно разделить по вертикали к пластине на три области: 1) область, непосредственно прилегающую к стенке с резким преобладанием вязкого трения; 2) область на некотором удалении от стенки с преобладанием турбулентного трения; 3) промежуточную или переходную область, в которой вязкое (молекулярное) и турбулентное трение соизмеримы. Эксперимент подтверждает наличие этих трех областей.
Если для удобства ограничиться все-таки наличием лишь двух областей: вязкого подслоя и турбулентного ядра, и воспользоваться методом размерностей, считая толщину подслоя степенной одночленной функцией от величин, ее определяющих - вязкости m, плотности среды r и напряжения трения на стенке tw, то получим:

Используя размерности m, r, tw и имея в виду, что a- безразмерная константа, будем иметь уравнение для размерностей в следующем виде:

или

Сравнивая показатели степеней в уравнении справа и слева (приравнивая их), получим следующую систему:
для [м] 1 = -a -3b - c,
для [кг] 0 = a + b + c,
для [с] 0 = -a - 2c.
Эта система имеет единственное решение: a = 1, b = c = -½. Отсюда окончательно получим, что толщина ламинарного подслоя равна

Для получения общепринятых формул введем следующие обозначения:

Величина

Величина


Если воспользоваться введенными обозначениями (2.27), то толщина подслоя

Полагая, что в подслое величина скорости есть линейная функция от "у", и пользуясь формулой



или

Таким образом, получены граничные условия (при у= dл =



Отсюда:

Подставив значение "С" в формулу(2.25), получим

Разделив обе части равенства на


Так как


или окончательно:

Переходя от натуральных к десятичным логарифмам, будем иметь:

Таким образом, учитывая, что a и æ - константы, получим закон распределения скоростей в турбулентном потоке:

где А и В - некоторые постоянные, определяемые через универсальные постоянные турбулентного движения a и æ следующим образом:

2.5. Математическое моделирование турбулентного течения
несжимаемой жидкости в трубах
При ламинарном движении полученные теоретические решения для труб хорошо совпадают с результатами опытов. Для турбулентного движения в трубах точного теоретического решения не существует и все закономерности получены либо из опытов, либо имеют полуэмпирический характер.
Рассмотрим профили скоростей при турбулентном движении в трубе. Между законом сопротивления и характером профиля скоростей в трубе существует однозначная связь, т.е. каждому профилю скоростей соответствует свой закон сопротивления, и наоборот.
Для получения закона распределения скоростей по радиусу трубы будем полагать, что, так же, как и для бесконечной пластины, в непосредственной близости от стенки трубы имеет место ламинарный подслой, в котором скорость - линейная функция от "у":

и что профиль скоростей в остальной части трубы подчиняется закону:

где А и В выражаются через универсальные газовые постоянные a и æ.
Известный ученый Никурадзе из анализа опытов с турбулентным потоком в круглой трубе при числах



Из опытов получено, что нижний предел





Измерения показали, что вблизи центра трубы распределение скоростей несколько отлично от логарифмического, но это отличие не очень существенно и в практических расчетах не учитывается. Можно считать, что логарифмический профиль скоростей является универсальным, пригодным для широкого диапазона чисел Re.
Вычислим далее так же, как и для ламинарного движения, максимальную




Вычитая из этой формулы значение


или

Здесь æ=0.4 по Никурадзе. Тогда

Величина средней скорости


Подставив под интеграл величину скорости по формуле

и разделив обе части выражения для



Таким образом, получим зависимость:

Если взять выражение для



В отличие от ламинарного движения в круглой трубе, при котором

Более простым, но далеко не универсальным профилем скоростей при турбулентном движении в трубе является так называемый степенной профиль:

Этот степенной профиль скоростей при числах Re»5×104
имеет вид:

и получил название закона одной седьмой.
Экспериментально было показано, что величина показателя степени "n" зависит от числа Re и с его увеличением падает. Оказалось возможным каждому числу Re подобрать такой показатель степени "n", чтобы полученный профиль скоростей наилучшим образом совпадал с результатами эксперимента.
Отношение максимальной к средней по сечению скорости при степенном профиле может быть найдено следующим образом. Определив


найдем:

или окончательно:

Результаты расчетов при различных "n" можно свести в таблицу:
|
n |
1/6 |
1/7 |
1/8 |
1/9 |
1/10 |
 |
1.264 |
1.224 |
1.194 |
1.173 |
1.156 |

Аналогично обычному степенному закону можно ввести степенное распределение скоростей в виде:

Значение коэффициента А можно определить из граничных условий на границе ламинарного подслоя: при y=dл скорость ux=uxл и постоянная





Зная величину a и задаваясь показателем n, можно получить численное значение постоянной А. Если a=11.5, то при n=1/7 А=8.74, и следовательно:

Надо отметить, что такое распределение скоростей при n=1/7 хорошо совпадает с экспериментом лишь в области Re £ 105, в то время как логарифмический профиль скоростей, который является универсальным законом, дает хорошее совпадение с экспериментом во всем диапазоне скоростей.
Рассмотрим законы сопротивления при турбулентном движении в трубах. Как уже было сказано, между профилем скоростей в трубе и законом сопротивления существует однозначная связь, т.е. каждому профилю скоростей соответствует свой закон сопротивления, и наоборот.
Блазиус предложил степенной закон сопротивления в виде:

где l - коэффициент сопротивления; а = 0.3164; m = 0.25 ( при Reкр < Re < 5.104).
Более поздние опыты показали, что численные значения в законе сопротивления зависят от числа Re. Чтобы в этом убедиться, рассмотрим связь динамической скорости


означающее, что движущийся перепад уравновешивается сопротивлением трения. С другой стороны:

В этих формулах DP - перепад давления на участке трубы длиной l; D - диаметр трубы;

Подставив DP из формулы (2.37) в формулу (2.36), получим:

Откуда величина напряжения на стенке tw равна:

или

Из последней формулы следует, что

тогда

Если применить формулу степенного профиля скорости




откуда

После преобразования найдем:

Отсюда

Воспользовавшись выражениями, полученными ранее:


после простых преобразований получим:

Сравнивая это выражение с формулой Блазиуса:


Отсюда следует, что закону сопротивления Блазиуса, в котором m=1/4, соответствует закон одной седьмой для профиля скорости.
Более универсальным, пригодным для всего диапазона чисел Re, является логарифмический закон сопротивления. Этот закон соответствует логарифмическому профилю скоростей и легко может быть получен.
Представим формулу для максимальной скорости турбулентного движения при логарифмическом профиле скоростей

в виде:

Так как





Окончательно, логарифмический закон сопротивления имеет вид:

где А1»2, В1»-0.8.
Многочисленные опыты Нуссельта, Никурадзе и др. подтверждают эту формулу с округленными коэффициентами:

Эта формула для использования неудобна, так как зависимость lот числа Re дана в неявном виде. Никурадзе предложил пользоваться следующей явной зависимостью:

(для напоминания: при ламинарном движении l=64/Re).
Один из вариантов расчета установившегося движения жидкости в круглой трубе таков:
а) задаются длина l и диаметр трубы D, кинематический коэффициент вязкости жидкости n и потребный расход жидкости Q,
б) по расходу и диаметру находим среднюю скорость


в) находим коэффициент сопротивления:

г) находим перепад давления DP на заданном участке трубы длины l:

д) находим сопротивление трения


е) определяем логарифмический профиль скоростей в трубе по формуле:

Задача решена.
Наряду с законами сопротивления, соответствующими степенному профилю скоростей



где

Запишем данную зависимость для оси трубы (y=R):


Вспоминая выражение для



Тогда закон сопротивления будет иметь вид:

В результате получаем для так называемого коэффициента местного сопротивления

где

Для наиболее распространенного профиля скоростей - закона одной седьмой (n=1/7; A=8.74) - закон сопротивления будет иметь вид:

или

В отличие от предыдущих законов сопротивления, в которых дана зависимость l(Re), в формуле (2.38) дается зависимость местного коэффициента сопротивления

Практика показывает, что законы сопротивления при турбулентном движении в трубах круглого сечения можно использовать и для расчета потерь в трубах любого поперечного сечения, если число Re выражать через гидравлический радиус


2.6 Математическая модель турбулентного пограничного
слоя на пластине
Вид уравнений движения и импульсов в турбулентном пограничном слое остается таким же, как и для ламинарного пограничного слоя, но значения d, d*, d** и tw будут иными.
Уравнение импульсов:

В основу полуэмпирической теории турбулентного пограничного слоя положена аналогия между турбулентным движением жидкости в трубе и в пограничном слое. При рассмотрении задачи о движении жидкости в трубе и в ламинарном пограничном слое было установлено, что:
а) давление зависит от продольной координаты и не зависит от радиуса трубы и от расстояния по нормали к стенке в пограничном слое;
б) скорости на стенке в обоих случаях равны нулю;
в) в трубе скорость достигает наибольшего своего значения на оси, а в пограничном слое - на его границе;
Отсюда можно заключить, что радиусу трубы и скорости на оси в трубе соответствует толщина слоя d и скорость u¥ на границе в пограничном слое. Эти соотношения можно применить и к осредненному движению. Тогда профили скоростей в турбулентном пограничном слое могут быть представлены в виде степенного или логарифмического законов, полученных ранее для труб.
1) Найдем сопротивление продольно обтекаемой пластины, воспользовавшись степенным законом:

Введя обозначение


При n=1/7, т.е. при законе одной седьмой


Для установления связи между tw и d воспользуемся степенным законом сопротивления, полученным для турбулентного движения в трубе.

Заменив в этом уравнении R на d и umax на u¥, получим

Подставив полученные выражения для d** и tw в уравнение импульсов, будем иметь:

Преобразуем это уравнение к виду

Теперь проинтегрируем это уравнение, используя следующее граничное условие: при х=0 d=0, означающее, что турбулентный пограничный слой начинается с передней кромки пластины.

При х=0 d=0, следовательно, С=0, и тогда


или окончательно получим:


Видно, что для турбулентного пограничного слоя характерные толщины слоя пропорциональны х4/5, в то время как для ламинарного пограничного слоя они пропорциональны




Коэффициент местного сопротивления трения пластины будет иметь вид:

т.е.

Найдем величину полного сопротивления Rx пластины (с двух сторон). Оно равно:

где b - ширина пластины.
Подставляя выражение для tw в виде:

получим

Проинтегрируем это выражение:


Окончательно:


Коэффициент полного сопротивления (см. формулу (1.29)) равен:

Подставляя значение Rx, получаем

Сравнение с экспериментом показало, что в последней формуле лучше взять коэффициент не 0.072, а 0.074, т.е.

Сравнение коэффициентов полного сопротивления при турбулентном


Например, при Re=106



Отсюда следует важный практический вывод: для уменьшения сопротивления трения обтекаемого тела необходимо добиться увеличения участка ламинарного пограничного слоя (рис. 12) и уменьшения участка турбулентного, т.е. необходимо затягивать как можно дальше ламинарное обтекание профиля{8].

Связь между коэффициентом сопротивления трения при турбулентном погранслое и общим коэффициентом сопротивления трения обтекаемого тела Cf можно выразить как


Это выражение можно записать по другому:


Толщина ламинарного пограничного слоя


Отсюда

Величина хкр, а следовательно и dл кр определяется из выражения для числа

2) Логарифмический профиль скоростей для турбулентного пограничного слоя, полученный по аналогии с турбулентным движением в трубе имеет вид.

Закон сопротивления, соответствующий логарифмическому профилю скоростей, довольно сложен. Коэффициент местного сопротивления трения в данном случае выражается зависимостью:

Коэффициент полного сопротивления трения:


2.7. Математическое моделирование обтекания турбулентным потоком
профиля произвольной формы
Отсутствие строгих теоретических основ турбулентного движения привело к появлению значительного количества полуэмпирических методов расчета турбулентного пограничного слоя на профиле. Изложим так называемый однопараметрический метод расчета[3]. Он выгодно отличается своей простотой и глубокой связью с методом такого же расчета ламинарного пограничного слоя.
В турбулентном погранслое так же, как и в ламинарном, вводится формпараметр. Уравнение импульсов здесь имеет такой же вид, как и для ламинарного пограничного слоя. Допуская, что кривые зависимостей H(f) и z(f) подобны в ламинарном и турбулентном пограничных слоях, получим простое решение задачи.
В отличие от ламинарного слоя, в котором формпараметр f и параметр z имели вид:

где

для турбулентного пограничного слоя в целях большей независимости решения от числа Re вводится более общий вид указанных величин:

где G(Re**) - некоторая функция от Re**, вид которой будет получен далее.
Выразим уравнение импульсов (1.26) через f и z следующим образом:


Умножив это уравнение на G(Re**), получим:

Преобразуем первое слагаемое, представив его через производную от произведения G(Re**)×d**.Тогда:




Введем величину,


или

Найдем отсюда член

и подставим его в уравнение импульсов (2.39). Тогда

Отсюда

или

Раскрывая производную в левой части, получим:


Подставляя это выражение в уравнение (2.40), получим:

или
где

Это уравнение ничем не отличается от своего ламинарного аналога (дифференциального уравнения формпараметра (1.31)), которое являлось основным для расчета ламинарного пограничного слоя на крыловом профиле произвольной формы. Различие заключается лишь в виде функциональной зависимости F(f). Если в выражении (2.41) для турбулентного погранслоя положить m=1, то оно совпадает с выражением для F(f) ламинарного пограничного слоя (см. уравнение (1.30)).
Величина G(Re**) принимается обратно пропорциональной местному коэффициенту сопротивления трения пластины, для которой


Из формулы


Таким образом, можно принять


При этом видно, что численное значение коэффициента пропорциональности


Воспользовавшись этим законом, получим:

Следовательно, формпараметр f и параметр z будут иметь вид:


Функция m при выбранном G(Re**) равна:

Это соотношение получается следующим образом: из формулы


Тогда


Линеаризуем функцию F(f), положив, как и для пластины,


Принимая эти значения z и H, найдем для F(f) линейное представление F(f)=a-bf, аналогичное представлению функции F(f) для ламинарного погранслоя, но с другими величинами постоянных a и b, равными для турбулентного погранслоя a=7/6 и b=4.7¸4.8.
Тогда уравнение импульсов для турбулентного погранслоя (2.41) можно представить в виде:

не отличающемуся по виду от соответствующего уравнения для ламинарного пограничного слоя и имеющего лишь другие численные значения для коэффициентов a и b.
Решением этого линейного дифференциального уравнения первого порядка является интеграл (решение в виде простой квадратуры):

Если турбулентный погранслой возникает с начальной точки профиля т.е. ламинарный участок отсутствует, то С=0 (так как при х=0, u¥=0) и

Так как в числитель и знаменатель в правой части равенства входит скорость, то , следовательно, начальная точка (х=0), в которой скорость равна нулю, есть особая точка. Раскрывая неопределенность, получим

Покажем это. Раскрытие неопределенности вида




Согласно правилу Лопиталя:


Пои наличии участка ламинарного пограничного слоя в интервале абсцисс (0<x<xкр), выражение для f(x) несколько усложняется и принимает вид:

Здесь индексом "кр" обозначены соответствующие величины в точке перехода ламинарного погранслоя в турбулентный. Значение формпараметра

Приняв


Согласно принятому условию смыкания ламинарного и турбулентного пограничных слоев, величина


а затем

Для проверки:

Зная Re**, можно найти


При z=1

И, наконец, находим местный коэффициент трения Сf,x из соотношения

аналогичного формуле для пластины, но при Re**, рассчитанном для заданного распределения скорости внешнего потока

Может представить интерес определение толщины вытеснения d*. В принятом приближении эта величина равна:

Таким образом, все параметры потока, в том числе полное сопротивление трения, могут быть определены. Надо подчеркнуть, что изложенный выше эмпирический подход, во многом опирающийся на аналогию с задачей о турбулентном пограничном слое на пластине, т.е. на случай постоянства скорости на внешней границе пограничного слоя, при своей простоте не уступает по точности результатов расчета другим, более совершенным методам.
Так как при безотрывном обтекании профиля сопротивление будет определяться почти полностью трением, то, очевидно, в этом случае для уменьшения сопротивления необходимо увеличивать участок ламинарного пограничного слоя. Иначе обстоит дало с плохо обтекаемыми телами, для которых характерно отрывное обтекание. Отрыв турбулентного погранслоя происходит позже, чем ламинарного, затягивание точки отрыва турбулентного слоя существенно влияет на уменьшение величины полного сопротивления плохо обтекаемых тел (таких, как шар или поперечно обтекаемый цилиндр), поскольку при отрыве потока сопротивление возрастает.
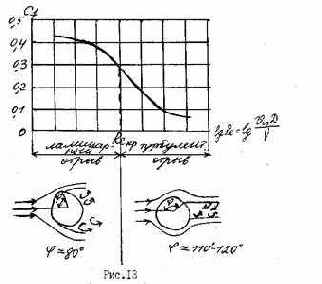
На рис. 13 показана кривая коэффициента сопротивления шара в зависимости от числа Re набегающего потока. Видно, что при достижении критического числа Рейнольдса (Reкр) происходит падение коэффициента сопротивления. Это явление называется кризисом обтекания плохо обтекаемых тел, сущность которого состоит в следующем.
Сопротивление плохо обтекаемых тел определяется прежде всего сопротивлением давления, которое зависит от величины области отрыва, а именно, чем больше область отрыва, т.е. чем раньше отрывается поток, тем больше сопротивление. При докритических числах Рейнольдса отрывается ламинарный слой и точка отрыва в этом случае расположена пол углом j » 80°. При увеличении числа Re до критического, т.е. при Re=Reкр точка перехода ламинарного погранслоя в турбулентный совпадает с точкой отрыва. Таким образом, при значениях Re³Reкр отрывается уже не ламинарный пограничный слой, а турбулентный.
При этом точка отрыва расположена при j »110°-120°. Причиной такого затянутого отрыва турбулентного пограничного слоя по сравнению с ламинарным является то обстоятельство, что наличие турбулентных пульсаций приводит к более интенсивному обмену энергией между пограничным слоем и внешним потоком, в результате чего кинетическая энергия частиц жидкости в пограничном слое увеличивается. Причина отмеченного явления резкого уменьшения сопротивления шара видна из кривых распределения давлений по его поверхности (см.рис.14).
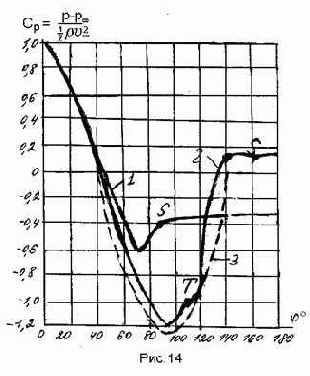 |
S - точка отрыва потока Т - точка перехода ламинарного погранслоя в турбулентный 1. Ламинарный отрыв:  Сх=0,47 2. Турбулентный отрыв Re=4,2×105; Cx=0,14 3. Идеальное распределение давлений |
Таким образом, для уменьшения сопротивления плохо обтекаемых тел надо уменьшать величину ламинарного участка с тем, чтобы отрывался турбулентный слой, (точка отрыва у которого расположена далее по потоку).
2.8 Профильное сопротивление
Расчет турбулентного пограничного слоя лежит в основе определения сопротивления тела при его движении в вязкой жидкости. Полное сопротивление (его называют еще лобовым) складывается из профильного
сопротивления и индуктивного сопротивления. Индуктивное сопротивление обусловлено конечностью размаха тела (неплоским характером обтекания), вследствие чего местная подъемная сила может давать отличную от нуля проекцию на направление общего набегающего потока.
Профильное сопротивление состоит из сопротивления трения и сопротивления давления. Сопротивление трения определяется как проекция на направление движения главного вектора касательных сил, приложенных со стороны жидкости к поверхности тела, а сопротивление давления - соответственно аналогичной проекцией главного вектора нормальных сил. Во многих случаях даже при безотрывном обтекании сопротивление трения не составляет основную часть профильного сопротивления. Поэтому во многих задачах при безотрывном обтекании необходимо знать профильное сопротивление, т.е. сопротивление трения плюс сопротивление давления.
Рассмотрим чуть подробнее вторую составляющую профильного сопротивления. Согласно общему для ламинарного и турбулентного пограничных слоев представлению, вне области пограничного слоя поток может рассматриваться как движущаяся безвихревым образом идеальная, т.е. лишенная вязкого трения, жидкость. При достаточной тонкости погранслоя и известном его свойстве передавать без изменения по сечениям слоя на поверхность тела давление внешнего (по отношению к пограничному слою) потока - главный вектор нормальных сил, согласно парадоксу Даламбера, должен быть равен нулю, а следовательно, и сопротивление давления не должно отличаться от нуля. Это было бы близко к действительности, если бы пограничный слой не возмущал внешний безвихревой поток. На самом же деле линии тока вследствие подтормаживающего влияния стенки оттесняются от поверхности тела на величину d* , называемую толщиной вытеснения и равную смещению действительной линии тока относительно линии тока безвихревого обтекания тела идеальной жидкостью на внешней границе пограничного слоя.
На поверхности обтекаемого тела (у=0) смещение линии тока исчезает, у обоих сравниваемых потоков (действительного и идеального) общая нулевая линия тока совпадает с поверхностью тела. При удалении от поверхности врыла смещения действительных линий тока по отношению к идеальным возрастают, и на границе пограничного слоя ( у=d) эта величина смещения достигает своего максимального значения.
Такое искажение картины течения приводит к нарушению идеального распределения давлений по поверхности тела. Таким образом, пограничный слой не только управляется внешним потоком, но и оказывает на него обратное влияние, которое проявляется особенно сильно на тех участках пограничного слоя, где слой наиболее толст, например, вблизи точки отрыва или в конце тела.
Как показывают опыты, сопротивление давления хорошо обтекаемого
крылового профиля при наличии на его поверхности полностью ламинарного или полностью турбулентного пограничного слоя убывает с ростом числа Re, т.к. при этом толщина погранслоя уменьшается и внешний поток приближается к безвихревому обтеканию профиля идеальной жидкостью.
Выражение коэффициента профильного сопротивления Схр
крылового профиля в безграничном плоском потоке жидкости через толщину потери импульса на бесконечности


где b -хорда крылового профиля; Rx - профильное сопротивление.
Эта формула непосредственно не может быть использована ввиду невозможности определения толщины потери импульса

Для установления указанной связи применим к следу за обтекаемым телом интегральное соотношение пограничного слоя. Так как в следе tw =0 ввиду отсутствия стенки, то интегральное соотношение Кармана для нашего случая примет вид:

Делим это уравнение на d** и интегрируем его по х вдоль следа от задней кромки (индекс "к") до бесконечно удаленного сечения вниз по потоку (индекс "¥"), получаем:

Для вычисления последнего интеграла необходимо знать зависимость


После подстановки найденного значения в интеграл последнее уравнение будет иметь вид:


Освобождаясь от логарифмов, запишем

Подставляя полученное выражение


Так как на бесконечности за телом поле скоростей будет выравниваться, можно считать, что



Так как



Подставив эти выражения в формулу для


Таким образом

на задней кромке меняется от 1.3-1.4 для продольно обтекаемой пластины и 1.8 - 2.0 - для толстых профилей. Обычно берут Нк=1.4 и тогда формула (2.43) для коэффициента профильного сопротивления будет иметь окончательный вид:

Эта известная формула Сквайра и Юнга, дающая хорошее совпадение расчетов с опытными материалами для широкого класса обтекаемых профилей.