Команда \newcommand со звездочкой
У команд \newcommand и \renewcommand существуют варианты " со звездочкой", называемые \newcommand* и \renewcommand. Они работают точно так же, как их тезки без звездочек, со следующим отличием: если команда с аргументами определена с помощью \newcommand* или \renewcommand*, то в ее аргументе не может содержаться пустая строка или команда \par. Если ваша команда определена с помощью \newcommand или \renewcommand без звездочки, то никаких ограничений на этот счет нет.
Смысл этого запрета таков. В большинстве случаев команды с аргументами, которые вы определяете, все равно не будут предусматривать подстановку вместо аргумента фрагмента текста, содержащего пустую строку или \par, так что этот запрет ни на чем не скажется (во всех примерах, приведенных в этой книге к настоящему моменту, можно совершенно безболезненно заменить \newcommand и \renewcommand на их варианты " со звездочкой"). А вот диагностика ошибок при наличии такого запрета облегчается. В самом деле, представим себе, что вы забыли набрать закрывающую фигурную скобку в аргументе команды (весьма распространенная ошибка!), как в следующем примере (забыта фигурная скобка в самой первой формуле; команду \smb мы определили в учебных целях раньше):
Символ Лежандра $\smb{a{l}$, где $a$ не делится на $l$, равен по определению $1$, если $a$ является квадратичным вычетом по модулю $l$, и $-1$ в противном случае. Вопрос о том, как зависит $\smb{a}{l}$ от $l$ при фиксированном $a$, является весьма важным и трудным. Великий немецкий математик К.-Ф.Гаусс...Если пустые строки в аргументе команды \smb не запрещены (так оно и будет, если определять \smb с помощью \newcommand без звездочки), то TeX будет терпеливо ждать, когда ему встретится закрывающая фигурная скобка, парная к первой из открывающих фигурных скобок в первой строке, а пока таковой нет — рассматривать весь читаемый им текст как составную часть первого аргумента команды \smb. В конце концов TeX либо доложит, что он прочел уже весь файл, а закрывающей фигурной скобки так и не нашел, либо прервет работу, объявив, что ему не хватило памяти.
Если же мы определим \smb с помощью \newcommand*, написав
\newcommand*{\smb}[2]{\left(\frac{#1}{#2}\right)} то ошибка не пойдет дальше текущего абзаца: как только TeX увидит пустую строку среди текста, рассматриваемого им как аргумент команды, он тут же прервет дальнейшее чтение и выдаст следующее стандартное сообщение об ошибке:
Runaway argument? {a{l}$, где$a$ не делится на $l$, равен п\ETC. ! Paragraph ended before \smb was complete. <to be read again> \par l.8 ? Нажав пару раз на "ввод", мы сможем благополучно продолжить обработку текста. В первом абзаце пропадет все после слов "Символ Лежандра", зато второй и последующие абзацы будут обработаны нормально (пока TeX не наткнется на очередную ошибку...).
Команды \newcommand и \renewcommand* обладают еще одним преимуществом перед своими вариантами без звездочек: при их использовании происходит (небольшая) экономия памяти.
Рекомендуем вам определять и переопределять команды с аргументами при помощи \newcommand* и \renewcommand*. Варианты без звездочек используйте только тогда, когда вы действительно намерены подставлять в аргумент своего макроса текст, состоящий из нескольких абзацев.
Команды без аргументов
Начнем с примера. Пусть вы пишете текст, в котором регулярно встречается математический значок

Часто писать такой длинный набор команд утомительно. Вот бы в LaTeX'е была предусмотрена команда, скажем, \eqdef, генерирующая символ бинарного отношения

После того как TeX прочтет эту строку, он всюду, встречая команду \eqdef, будет реагировать точно так же, как если бы он видел текст \stackrel{\mathrm{def}}{=}. Например, формула

Новая команда TeX'а, которую мы определили, называется макросом (еще говорят: макроопределение, макрокоманда, макро). Рассмотрим точные правила для создания макросов средствами LaTeX'а.
Для создания макросов используется команда \newcommand. Эта команда имеет два обязательных аргумента. Первый из них — имя, которое вы придумали для вашего макроса. Имена макросов должны подчиняться тем же правилам, что имена TeX'овских команд, либо backslash и после него одна не-буква, либо backslash и после него — последовательность букв. Второй обязательный аргумент команды \newcommand, называемый " замещающим текстом", сообщает TeX'у смысл макроса: на этот текст ваш макрос будет замещаться в процессе трансляции (как говорят, макрос будет "разворачиваться").
При пользовании командой \newcommand нельзя в качестве имени макроса выбирать имя уже существующей команды или окружения (если вы попробуете так сделать, LaTeX выдаст сообщение об ошибке).
Во втором аргументе команды \newcommand (иными словами, в "замещающем тексте") вместе с каждой открывающей фигурной скобкой должна присутствовать соответствующая ей закрывающая1), так что определения наподобие
\newcommand{\nachatkursiv}} \newcommand{\konchitkursiv}{}} приведут в лучшем случае к сообщению об ошибке (и желаемого эффекта не дадут). Если вам кажется, что такие ограничения стеснительны, можете изучить по книге [2], как их обходить; для большинства практических целей возможности создания макроопределений, предоставляемые LaTeX'ом, вполне достаточны.
К сожалению, некоторые русификации TeX'а не позволяют использовать в именах макросов русские буквы.
Еще одно ограничение: имя новой команды не должно начинаться на end.
Наконец, в замещающем тексте макроопределения нельзя пользоваться командой \verb или окружением {verbatim}.
Если команда \newcommand дана внутри группы, то смысл определяемой ею новой команды будет забыт TeX'ом по выходе из группы. Если новая команда определяется в преамбуле, то, естественно, она будет понятна TeX'у на протяжении всего документа.
Давайте теперь разберем несколько примеров, обращая внимание на типичные ошибки.
Макросы хороши как средство скорописи. Например, если в вашем тексте часто встречается знак

\newcommand{\btu}{\bigtriangleup} и вы сможете писать формулы наподобие

В лекции 2 вы найдете массу других примеров громоздких конструкций, для которых имеет смысл создать макросы.
А теперь — пример типичной ошибки. Пусть в тексте, который вы набираете, регулярно встречаются фразы наподобие
Подмногообразия проективного пространства

\newcommand{\Pn}{$\mathbf P^n$} Теперь можно писать, например, так:
... пространства~\Pn{} - основной объект... Однако для набора формулы

Причина проста: TeX исправно подставляет вместо \Pn тот "замещающий текст", который вы ему сообщили во втором аргументе команды \newcommand. В результате этого при развертывании макроса \Pn текст $x\in\Pn$ превращается в незаконный текст $x\in$\mathbf P^n$$, в котором математическая формула заканчивается со вторым из знаков доллара, а символ ^ оказывается посреди обычного текста. Чтобы можно было напечатать

\newcommand{\Pn}{\mathbf{P}^n} При этом придется, конечно, ставить знаки доллара вокруг \Pn в тех случаях, когда в тексте встречается просто

Есть, впрочем, и более удачный способ борьбы с этой проблемой: определите\Pn как
\newcommand{\Pn}{\ensuremath{\mathbf{P}^n}} (без всяких знаков доллара) — и вы сможете спокойно пользоваться своей новой командой \Pn как в тексте, так и в формулах:
Пусть \Pn~ — $n$---мерное проективное пространство, а $X\subset \Pn$~ — неприводимое многообразие... (знаки ~ мы поставили, чтобы строчка не смогла начаться с тире —c.103). Команда \ensuremath всегда обрабатывает свой аргумент как математическую формулу, независимо от того, в тексте или в формуле вы ее используете.
Создавать макросы полезно не только для сокращения числа нажатий на клавиши при наборе формул. Вот пример, когда макросы помогают и при наборе обычного текста. Предположим, в нашем тексте много задач, причем условие каждой из задач начинает новый абзац (как обычно и бывает). Предположим также (временно), что эти задачи никак не нумеруются. Слово "Задача", с которого начинается условие, хочется как-то выделить в тексте; предположим, мы решили выделять его жирным шрифтом. Давайте создадим макрос, который будет делать все это за нас, чтобы можно было не печатать каждый раз слово "Задача", а просто написать \z. Первым обычно приходит в голову что-нибудь такое:
\newcommand{\z}{\bfseries Задача} Посмотрите, что из этого выйдет:
 | \z. Пять парней за пять дней съели пять окуней. За сколько дней пятнадцать парней съедят пятнадцать окуней? |
p> Почему же жирным шрифтом напечаталось не только слово "Задача", но и весь дальнейший текст? Ответ: TeX опять пунктуально заменил \z на "замещающий текст", в результате чего получилось вот что:
\bfseries Задача. Пять парней ... Команда \bfseries оказалась не внутри группы, и весь текст напечатался жирным шрифтом. Чтобы не попадаться в такую ловушку, надо помнить, что при развертывании макроса фигурные скобки, ограничивающие замещающий текст в команде \newcommand, отбрасываются. Правильнее было бы дать такое определение:
\newcommand{\z}{\bfseries {Задача}}" На сей раз \z будет заменяться на {\bfseries Задача} (отбрасывается внешняя пара фигурных скобок, ограничивающая второй аргумент команды \newcommand, и только она!). А можно (это, пожалуй, даже лучше) написать и так:
newcommand{\z}{\textbf{Задача}} Впрочем, наш макрос \z еще не идеален. Во-первых, после слова, напечатанного жирным шрифтом, точку лучше поставить тоже жирным шрифтом, поэтому разумно и ее включить в макроопределение. Далее, согласно общему правилу игнорирования пробелов после имени команды, состоящего из букв, в тексте при этом нельзя будет написать
\z Пять парней... так как при этом пропадет пробел между словом "Задача." и следующим словом. Можно этот пробел, как водится, всякий раз специально организовывать и писать
\z{} Пять парней... но лучше вставить и пробел прямо в определение:
\newcommand{\z}{\textbf{Задача. }} Теперь запись \z Пять парней... даст то, что нужно. Впрочем, если угодно, вот еще один штрих. Если вы в какой-нибудь момент забудете оставить пустую строку перед очередной задачей, то слово "Задача" при этом будет не начинать абзац, а продолжать предшествующий текст. Чтобы этого раз и навсегда избежать, можно вставить команду "закончить абзац" в наше макроопределение. Как вы помните, эта команда называется \par:
\newcommand{\z}{\par\textbf{Задача. }} Если перед нашим макросом \z пустая строка все-таки будет, то лишняя команда \par ни на что не повлияет, а если ее не будет, то \par сыграет роль недостающей пустой строки.
Если какой-то элемент текста оформлен с помощью макроса, становится удобно менять это оформление. Например, если вдруг понадобилось оформлять все задачи так, чтобы соответствующие абзацы начинались без отступа, достаточно внести небольшое изменение в наше определение команды \z:
\newcommand{\z}{\par\noindent\textbf{Задача. }} Если бы каждую задачу мы оформляли вручную, нам пришлось бы перед каждым словом "Задача" вписывать команду \noindent. В дальнейшем, познакомившись с LaTeX'овскими " счетчиками", мы усовершенствуем наш макрос \z таким образом, чтобы он еще и автоматически нумеровал задачи.
Мы уже говорили, что переопределить значение уже существующей команды с помощью \newcommand невозможно. Иногда, однако, это бывает необходимо. Пример тому приведен в лекции 3 : если мы хотим, чтобы в заголовках глав печаталось именно слово "Глава", а не " Chapter", то необходимо определить по-новому команду \chaptername. Для такого рода целей используется команда \renewcommand. Она устроена точно так же, как \newcommand, с тем отличием, что в качестве ее первого аргумента надо указывать имя уже существующей команды; в этом случае по выполнении команды \newcommand значение этой команды изменится: она превратится в сокращенное обозначение для текста, указанного в качестве ее второго аргумента. Например, если написать
\renewcommand{\alpha}{Ку-ку} то команда \alpha будет генерировать не то, что обычно (букву

Если команда \renewcommand дана внутри группы, то созданное ею переопределение значения команды забудется по выходе из этой группы. Если в качестве первого аргумента команды \renewcommand указать имя несуществующей команды, то вы получите сообщение об ошибке.
Команда \renewcommand при неаккуратном обращении может привести к неприятностям. Дело в том, что нередко команды LaTeX'а определяются в терминах других команд LaTeX'а, причем знать эти сложные связи рядовой пользователь вовсе не обязан.
На практике такое незнание может привести к тому, что безобидное на первый взгляд использование в своих целях имени какой-нибудь команды, которая в вашем тексте ни разу не встречается, вызовет необъяснимо неправильную работу других команд. Поэтому используйте \renewcommand только тогда, когда вы полностью отдаете себе отчет в своих действиях.
Выше мы часто называли макросы просто командами, и это — не просто небрежность речи: на самом деле принципиальной разницы между макросами и TeX'овскими командами почти нет. В частности, почти все команды LaTeX'а, о которых говорилось и еще будет говориться в нашей книге, являются именно макросами; в отличие от макросов, создаваемых нами с помощью \newcommand, их смысл уже известен TeX'у к моменту запуска программы, так что определять их каждый раз не нужно. Макросы, в свою очередь, могут ссылаться на другие макросы (кстати, команда \stackrel, на которую ссылалась наша команда \eqdef, также является макросом) - и так далее, пока не дойдет до так называемых "примитивных команд" TeX'а. Из команд, о которых мы вам рассказывали, примитивными являются считанные единицы: \left, \right, \noindent и некоторые другие.
Команды с аргументами
Мы уже научились создавать новые команды, не требующие аргументов. Но мы хорошо знаем, что многие LaTeX'овские команды принимают аргументы, и часто возникает потребность создать новую команду с такими возможностями. Пусть, например, в вашем тексте часто встречается "символ Лежандра", выглядящий так:

Хорошо бы создать команду \smb с двумя аргументами, чтобы можно было написать в формуле "\smb{a}{l}" и получить на печати

Разберем, что означает эта запись. В квадратных скобках стоит количество аргументов в нашем макросе (в нашем случае 2). Далее, в самом "замещающем тексте" появились значки "#1" и "#2" . При развертывании макроса на их место будут подставляться соответственно первый и второй аргументы нашей новой команды \smb. Например, если в формуле написать
\smb{a+b}{c}то будет напечатано

Теперь рассмотрим точные правила. Необязательный аргумент команды \newcommand, который должен быть расположен между двумя обязательными, указывает, сколько аргументов будет требовать создаваемая вами команда (макрос). Это количество аргументов не может быть более 9. В "замещающем тексте" места, на которые при развертывании макроса будут подставляться аргументы, обозначаются символами "#1" для первого аргумента, "#2" для второго аргумента и т.д. Эти символы могут идти в любом порядке и присутствовать любое количество раз (в том числе и ни разу). Когда мы будем использовать нашу новую команду в тексте, после ее имени в фигурных скобках должны будут следовать аргументы, ровно в том количестве и в том порядке, который мы указывали в необязательном аргументе команды \newcommand, каждый — в своей паре фигурных скобок (как обязательные аргументы любой другой LaTeX'овской команды).
При развертывании макроса на место его и его аргументов будет подставлен " замещающий текст", в котором вместо "#1" всюду стоит первый аргумент, вместо "#2" — второй аргумент и т.д.
Проиллюстрируем все сказанное примером. Пусть мы определили команду \shuffle следующим образом:
\newcommand{\shuffle}[4]{К#4к#2#1л} Тогда будет получаться, например, такое:
 | \shuffle{ди}{о}{го}{ро} Гена и его друзья. |
Ни аргументы LaTeX'овских команд (в том числе и определенных вами), ни "замещающий текст" в \newcommand не должны содержать "несбалансированных" (не имеющих пары) фигурных скобок (это не относится к \{ и \}).
Если вы хотите создать макрос с аргументами, имя которого совпадает с именем уже существующей команды, то надо воспользоваться командой \renewcommand с необязательным аргументом. Место постановки и значение этого необязательного аргумента, а также правила употребления символов #1, #2 и т.д. при этом будут такие же, как для команды \newcommand.
Приведем еще один пример практически полезного макроса с аргументами. При написании этой книги автор широко пользовался ссылками на страницу, автоматически генерируемыми с помощью команды \pageref. Например, если какое-то место в тексте было помечено с помощью команды \label{units}, то ссылка на соответствующую страницу выглядела так:
Как мы уже отмечали на с. \pageref{units}, ... После первого десятка таких ссылок возникает желание сократить число нажатий на клавиши. В результате в преамбуле появилась строка
\newcommand{\str}[1]{стр. \pageref{#1}} и ссылки на страницы стало возможно оформлять так:
Как мы уже отмечали на \str{units}, ... (Автор вначале не знал, что надо писать "с.", а не " стр.", но мгновенно исправился, всего лишь удалив две буквы из определения команды \str!)
Модификация оформления перечней
Начнем с {itemize}. Чтобы поменять значки, которыми помечаются элементы перечня, надо переопределить команду \labelitemi. Если, например, мы хотим, чтобы элементы перечня отмечались не черными кружками, а галочками

. Если окружение {itemize} расположено внутри другого окружения {itemize}, как в примере на {itemize}, то значки для пометки элементов перечня будут уже, вообще говоря, другими: их вид задается командой \labelitemii; вид значков для пометок элементов itemize на третьем и четвертом уровнях вложенности задается командами \labelitemiii и \labelitemiv; их также можно переопределять.
Правильнее было бы определять заголовки для itemize чуть хитрее. Например, наше определение \labelitemi лучше дать так:
\renewcommand{\labelitemi}{$\mathsurround=0pt \surd$}Если дать определение именно так, то вокруг галочки не появится дополнительный пробел даже в случае, если вы в какой-то момент решите установить ненулевое значение параметра \mathsurround. Поскольку формула образует группу, в дальнейшем предыдущее значение \mathsurround восстановится. Полезно иметь в виду этот прием, если вы пользуетесь математическими символами в качестве типографских значков.
Теперь рассмотрим окружение {enumerate}. Коль скоро оно автоматически нумерует элементы перечня, можно предположить, что это окружение связано с LaTeX'овскими счетчиками. Так оно на самом деле и есть: это окружение использует счетчик enumi. Если одно {enumerate} вложено в другое, то используются счетчики enumii, enumiii и enumiv для нумерации элементов перечня на втором, третьем и четвертом уровнях вложенности. С другой стороны, сами значки, помечающие элементы перечня, порождаются командами \labelenumi, \labelenumii, \labelenumiii и \labelenumiv — в зависимости от уровня вложенности. Например, команда \labelenumi определена так:
\newcommand{\labelenumi}{\theenumi.}в то время как the-команда, определяющая представление счетчика enumi на печати, определена просто как
\newcommand{\theenumi}{\arabic{enumi}}Стало быть, если мы не меняем стандартного стиля оформления, то элементы перечня {enumerate} (не вложенного в другой {enumerate}) будут нумероваться цифрами с точкой. Если же мы хотим, скажем, чтобы после цифры шла не точка, а скобка (как в нашей книге), то можно в преамбуле написать
\renewcommand{\labelenumi}{\theenumi)}Если же мы к тому же хотим, чтобы элементы перечня нумеровались римскими цифрами, то можно написать еще и так:
\renewcommand{\theenumi}{\Roman{enumi}}Аналогичным образом можно менять оформление нумерованных перечней на других уровнях вложенности.
Если вы хотите изменить оформление перечня более серьезным образом (например, установить другую величину полей, или сделать так, чтобы значки, помечающие элементы перечня, были выровнены по левому, а не по правому краю), то вам придется подождать до лекции 9.
Новые окружения: общий случай
Как мы уже имели возможность убедиться, для сокращения времени на написание длинных последовательностей команд удобно пользоваться макросами. В тех случаях, когда для достижения необходимого нам эффекта требуется сложная последовательность команд в начале и в конце какого-то текста, LaTeX дает возможность оформить соответствующие макросы в виде нового окружения. Как это делается, разберем на примере.
Предположим, нам хочется взять в рамку абзац текста шириной

При этом будет напечатано вот что:

Если таких рамок с текстом у вас много, то можно сократить число нажатий на клавиши, определив окружение с именем, скажем, {ramka}, так, чтоб можно было бы просто писать
\begin{ramka} Этот текст будет ... ... этих целей. \end{ramka}Определяется это окружение так:
\newenvironment{ramka}{\begin{tabular}{|p{7cm}|} \hline}{\\\hline\end{tabular}}В общем случае команда \newenvironment имеет такой формат:
\newenvironment{имя}{открывающие\_команды}{закрывающие\_команды}Здесь имя — имя определяемого окружения, открывающие\_команды — команды и/или текст, подставляемые вместо команды \begin с именем окружения, закрывающие\_команды — команды и/или текст, подставляемые вместо команды \end с именем окружения.
Вместо окружения, определяемого с помощью \newenvironment, можно с тем же успехом создать два макроса: один — для открывающих\_команд, другой — для закрывающих. Например, в нашем случае с рамкой можно было бы написать
\newcommand{\nachalo}{\begin{tabular}{|p{7cm}|}\hline} \newcommand{\konec}{\\\hline\end{tabular}}и создавать рамки так:
\nachalo Этот текст... \konecПреимущество оформления такого рода конструкций в виде окружений состоит в том, что при этом легче контролировать ошибки: если вы напишете \begin{ramka} и при этом забудете написать соответствующую команду \end{ramka}, то LaTeX выдаст сообщение об ошибке, в котором именно это вам и скажет; если же вы забудете команду \konec, то сообщения об ошибке будут менее понятными.
Кроме того, нелишне напомнить, что команды \begin и \end, ограничивающие окружение, ограничивают группу: все неглобальные определения и изменения параметров, происходящие внутри окружения, забываются по выходе из него.
Новые окружения можно определять так, чтобы они принимали аргументы. Пусть, например, в зависимости от обстоятельств нам нужны рамки разной ширины. Тогда разумно модифицировать определение окружения {ramka} таким образом, чтобы ширина текста в рамке передавалась ему как аргумент. Соответствующее определение будет выглядеть так:
\newenvironment{ramka}[1]{\begin{tabular}{|p{#1}|} \hline}{\\\hline\end{tabular}} После этого можно писать, например,
\begin{ramka}{6cm} Текст... \end{ramka} или даже
\begin{ramka}{.85\textwidth} Текст... \end{ramka} Общие правила таковы. Чтобы создать окружение с аргументами, надо воспользоваться командой \newenvironment c необязательным аргументом. Этот необязательный аргумент ставится между первым и вторым обязательными; как и в случае с \newcommand, он означает количество аргументов, которые будет требовать окружение, и это количество не может превышать девяти; места, куда будут вставлены аргументы, по-прежнему обозначаются #1,...,#9, причем эти значки можно употреблять только в открывающих командах (т.е. во втором обязательном аргументе команды \newenvironment)
С помощью \newenvironment нельзя переопределить уже существующее окружение (если вы все же попробуете так сделать, LaTeX выдаст сообщение об ошибке). Если вам действительно необходимо такое переопределение, надо пользоваться командой \renewenvironment, работающей точно так же, как и \newenvironment, с тем различием, что в качестве первого аргумента ей можно передавать только имя уже существующего окружения.
У команд для пере)пределения окружения также существуют " варианты со звездочкой": \newenvironment* и \renewenvironment*. Если окружение с аргументами определено с помощью одной из этих команд, то в его аргументе запрещены пустые строки или команды \par.
Окружения типа " теорема"
Если вы пишете математический текст, то в этом тексте будет содержаться немалое количество теорем, лемм, определений и тому подобных вещей. Эти элементы математического текста желательно оформлять специальным образом. Например, формулировки теорем часто печатают, для ясности, другим шрифтом, само слово "теорема" также выделяют (третьим) шрифтом и т.д. Чтобы задать такое оформление, в исходном тексте приходится написать довольно много TeX'овских команд, и лучше не повторять этот длинный набор команд много раз, а создать заменяющее его макроопределение, что, в свою очередь, может потребовать некоторого труда (чем-то подобным мы занимались в предыдущих разделах, когда разрабатывали команду \z). Если же вы или редакция, с которой вы имеете дело, не слишком требовательны к деталям оформления, то соответствующие макросы (точнее говоря, новые окружения) легко создать из полуфабрикатов, предоставляемых нам для этих целей LaTeX'ом.
Окружения, используемые в LaTeX'е для оформления фрагментов текста типа "теорема", заранее не определены. Дело в том, что количество различных типов объектов наподобие теоремы, присутствующих в одном тексте, может быть достаточно велико (предложение, утверждение, лемма, определение, замечание,...), так что LaTeX в целях экономии машинной памяти и исходя из того, что на все вкусы таких окружений все равно не напасешься, определять их предоставляет вам. Как это делать, удобнее всего разобрать на примере.
Пусть в нашем тексте присутствуют "предложения". Давайте создадим окружение {predl} таким образом, чтобы можно было, например, писать

Для создания такого окружения используется команда \newtheorem:
\newtheorem{predl}{Предложение}Как видите, команда \newtheorem имеет два обязательных аргумента: первый - название окружения, которое мы создаем, второй - заголовок нашей "теоремы".
Теперь обсудим, как работают окружения, созданные при помощи команды \newtheorem (будем называть их просто окружениями типа "теорема"). Во-первых, как вы уже заметили, формулировка печатается курсивом, а заголовок — полужирным шрифтом. Во-вторых, абзац, идущий после нашего окружения, начинается с абзацным отступом, если после закрывающей окружение команды \end идет пустая строка, и без отступа в противном случае (так что в этом отношении окружения типа "теорема" ведут себя совершенно аналогично таким окружениям, как {quote}, {itemize} и т.п.). В-третьих, окружение типа " теорема" может иметь необязательный аргумент (как обычно, в квадратных скобках). Текст, стоящий в этих квадратных скобках, будет напечатан в скобках после заголовка "теоремы" и ее номера. Обычно это используется для указания ученого, чьим именем названа "теорема":

Вместе с окружением типа "теорема" автоматически создается и счетчик, хранящий его номер. Имя этого счетчика совпадает с именем окружения (так что в нашем примере счетчик называется predl); чтобы изменить представление на печати номеров наших "теорем", можно обычным образом переопределить соответствующую the-команду. Например, если мы хотим, чтобы предложения нумеровались прописными латинскими буквами, надо в преамбуле написать:
\renewcommand{\thepredl}{\Alph{predl}} " Теоремы", определяемые описанным выше способом, будут иметь сплошную нумерацию на протяжении всего документа. Как мы уже понимаем, это далеко не всегда удобно. Часто хотелось бы сделать так, чтоб, например, в каждом разделе нумерация " теорем" начиналась заново. Для таких целей предусмотрена команда \newtheorem с необязательным аргументом. Этот аргумент ставится после двух обязательных и представляет собой имя того счетчика, которому будет подчинен счетчик нашей " теоремы".
Пусть, например, в нашем тексте есть не только предложения, но и теоремы (без кавычек), и мы хотим, чтобы нумерация теорем начиналась заново в каждом разделе. Тогда можно написать в преамбуле так:
\newtheorem{theorem}{Теорема}[section] После этого можно будет писать, например, вот что:

\newtheorem{xyz}[abcd] (счетчик "теоремы" типа xyz подчинен счетчику abcd) команда \thexyz будет определена как
\theabcd.\arabic{xyz} (если вы хотите, чтобы нумерация "теоремы" представлялась на печати иначе, вы опять-таки можете переопределить the-команду).
Наконец, LaTeX предоставляет еще одну возможность нумерации определяемых вами "теорем". Предположим, что кроме теорем в вашем тексте есть еще и леммы, и при этом вы хотите, чтобы леммы и теоремы нумеровались совместно: теорема 2.1, теорема 2.2, затем лемма 2.3, затем теорема 2.4 и т.д. Тогда, предполагая, что окружение {theorem} уже определено, как выше, можно определить окружение {lemma} так:
\newtheorem{lemma}[theorem]{Лемма} В этом случае необязательный аргумент команды \newtheorem располагается между двумя обязательными; этот аргумент - имя того окружения типа "теорема", совместно с которым будет нумероваться определяемая вами "теорема".
Команду \newtheorem можно использовать или с одним необязательным аргументом, или с другим, но не с обоими вместе.
Окружения типа "теорема" в пакете amsthm
Все LaTeX'овские "теоремы", определяемые пользователем при помощи окружения {newtheorem}, оформляются в одном и том же стиле, что не всегда приемлемо. Пакет {amsthm}, распространяемый Американским математическим обществом, позволяет внести в это оформление некоторое разнообразие. Итак, предположим, что вы его подключили. Что нового, по сравнению с "чистым" LaTeX'ом, можно сделать?
Во-первых, в этом пакете определен "вариант со звездочкой" команды \newtheorem. Именно, если определить очередной тип " теорем" с помощью \newtheorem* вместо \newtheorem, то "теоремы" указанного типа не будут нумероваться.
Во-вторых, для управления стилем оформления окружений типа "теорема" предназначена команда \theoremstyle, аргументом (единственным) которой может быть слово plain , definition или remark. Если в преамбуле дать эту команду с одним из трех допустимых аргументов, то все "теоремы", определяемые с помощью \newtheorem после этой команды \theoremstyle, будут оформлены в соответствующем стиле; чтоб определить тип теорем, оформляемый в другом стиле, надо написать еще одну команду\theoremstyle (с другим аргументом, разумеется), а уж после нее — очередную \newtheorem. Стиль plain рекомендуется для собственно теорем, предложениий и лемм, definition — для определений, remark — для замечаний3). Если в преамбуле нет ни одной команды \theoremstyle, подразумевается стиль plain.
В-третьих, в пакете amsthm предусмотрено также окружение proof, предназначенное для оформления доказательств. Это окружение автоматически ставит слово Proof в начало доказательства и автоматически же завершает доказательство символом


Окружение proof допускает и необязательный аргумент: если написать, скажем,
\begin{Proof}[Доказательство основной теоремы] то вместо слова Proof появится текст, записанный нами в квадратных скобках.
 |
 |
 |
2) Можно (и разумно) использовать в этой ситуации команду \newcommand* (" вариант со звездочкой"). См. по этому поводу ниже.
3) В стиле plain заголовок печатается жирным шрифтом, а текст " теоремы" — курсивом, в стиле definition заголовок печатается жирным шрифтом, а текст " определения" — прямым, в стиле remark заголовок печатается курсивом, а текст "замечания" — прямым шрифтом.

Организация автоматических ссылок
Вернемся последний раз к нашей команде \z. Раз она автоматически нумерует задачи, то неплохо было бы, если б пронумерованные ею задачи можно было метить командой \label и ссылаться на эти метки командой \ref ссылка на счетчик, определенный пользователем} (проблема именно в ней, поскольку команда \pageref, дающая номер страницы, сработает в любом случае). Если коротко, то решение этой проблемы таково: увеличивать на единицу значение счетчика \ctr{zadacha} надо не с помощью команды \addtocounter, которой мы пользовались до сих пор, а с помощью команды \refstepcounter, о которой уже шла речь по другому поводу в предыдущем разделе. Если мы определим команду \z так:
\newcommand{\z}{\par\refstepcounter{zadacha}% \textbf{Задача \arabic{section}.\arabic{zadacha}.} }то после этого можно будет написать, например, так:
\z Решить уравнение... \z Доказать...\label{prove} \z Найти сумму...Если теперь в другом месте текста мы сошлемся на помеченную задачу так:
В задаче \ref{prove} предлагалось доказать...то будет печататься ее номер (тот самый, который LaTeX автоматически ей присвоил). Впрочем, с такими автоматическими ссылками не все будет благополучно: если помеченная нами задача была второй по счету в разделе номер 3, то называться она будет Задача 3.2, а вот ссылка на нее, сгенерированная командой \ref, будет выглядеть просто
В задаче 2 предлагалось доказать...в то время как хотелось бы автоматически получить В задаче 3.2. Иными словами, надо изменить текст, генерируемый командой \ref. Чтобы узнать, как этого добиться, нам придется познакомиться с еще одной LaTeX'овской конструкцией, связанной со счетчиками.
Мы уже знаем, что значение LaTeX'овского счетчика можно вывести на печать командами \arabic, \roman и т.п. Однако, кроме этого, с каждым счетчиком связана индивидуальная команда, определяющая, в какой форме его значение будет выводиться на печать, и именно в соответствии с этой командой печатается ссылка, сгенерированная с помощью \label и \ref. Имя этой команды получается, если поставить the перед именем счетчика.
Например, команда для вывода на печать номера раздела называется \thesection, для вывода на печать номера главы — \thechapter, команды для вывода на печать определенных нами счетчиков slave и master — \theslave и \themaster. При создании счетчика автоматически определяется и соответствующая the-команда. Именно, при создании счетчика по имени, скажем, abcd автоматически определяется команда \theabcd таким образом:
\newcommand{\theabcd}{\arabic{abcd}} В дальнейшем эту команду можно переопределять:
 | \renewcommand{\theabcd}% {\Roman{abcd}} \setcounter{abcd}{14} Людовика \theabcd{} звали ``Король-Солнце''. |
\renewcommand{\thezadacha}{\thesection.\arabic{zadacha}} Если включить эту команду в преамбулу документа, то ссылки на сгенерированные нашей командой \z номера задач будут выглядеть должным образом.
В нашем переопределении команды \thezadacha мы воспользовались командой \thesection, чтобы наши макросы правильно работали с любым классом документов. Дело в том, что при разумном оформлении номер раздела, предшествующий при ссылке номеру задачи, должен печататься таким же образом, как и номер раздела при ссылке на раздел, а это в разных классах делается по-разному: в классе article, например, \thesection — это то же самое, что и \arabic{section} (иными словами, ссылка на раздел, сгенерированная командой \ref, печатает просто номер раздела), а в классе report команда \ref при печати ссылки на раздел печатает не номер раздела, а номер главы, точку и номер раздела. Поскольку мы написали \thesection, все эти тонкости будут учтены автоматически.
Приведем еще один (игрушечный) пример использования счетчиков в макроопределениях, отчасти чтобы еще раз продемонстрировать применение подчиненных счетчиков, а отчасти чтобы убедить читателя, что не боги горшки обжигают. Именно, давайте разработаем свои собственные команды для создания разделов документа, не полагаясь на \chapter, \section и т.п.
из стандартных LaTeX' овских классов. Для простоты предположим, что заголовки глав и разделов будут укладываться в одну строку, и не будем заботиться о том, насколько удачным выйдет оформление заголовков. Итак, пусть наш документ делится на главы, которые, в свою очередь, делятся на разделы. Каждую главу будем начинать с новой страницы, перед каждым разделом оставлять 1cm (если, конечно, раздел не начинает новой страницы). Наконец, предусмотрим, чтобы главы и разделы автоматически нумеровались с возможностью создания автоматических ссылок на эти номера. Команды для создания главы и раздела назовем \glava и \razdel; это будут команды, требующие одного аргумента — названия главы или раздела.
Чтобы номера глав и разделов генерировались автоматически, нам необходимо создать счетчики, содержащие эти номера. Пусть счетчик с номером главы называется glava, а счетчик с номером раздела — razdel (имена счетчиков могут совпадать с именами команд). Имея в виду, что нумерация разделов в каждой главе будет начинаться заново, напишем в преамбуле так:
\newcounter{glava} \newcounter{razdel}[glava] Теперь определим команду \glava:
\newcommand*{\glava}[1]{\clearpage % с новой страницы \vspace*{4cm}% оставить место сверху \refstepcounter{glava}% новый номер главы {\LARGE\rmfamily\bfseries\upshape % шрифт для заголовка Глава \theglava. #1% заголовок \par % кончить заголовок \vspace{5mm plus 1mm minus .5mm}% Промежуток между % заголовком и текстом }% завершить группу, внутри которой менялся шрифт }% конец макроопределения Поскольку номер главы устанавливается командой \refstepcounter, при этом будет начата заново и нумерация разделов, а на номера глав можно будет делать автоматические ссылки с помощью \label и \ref. В определении шрифта для заголовков мы в явном виде установили все четыре атрибута, чтобы быть уверенными, что он будет какой надо (если бы мы, например, не сказали \upshape, а предыдущая глава заканчивалась курсивом, определенным командой \itshape, данной вне группы, то заголовок напечатался бы жирным курсивом).
Обратите также внимание на команду \theglava. Мы воспользовались ею, поскольку не хотим на этом этапе предрешать, в каком виде номер главы будет представлен в заголовке: в виде арабской цифры, римской цифры или еще как-нибудь. Если в дальнейшем нам захочется изменить вид этого представления, то не придется менять, с риском ошибиться, длинное определение команды \glava, а будет достаточно переопределить команду \theglava. Заметьте, что промежуток между заголовком и текстом мы сделали растяжимым, чтобы помочь TeX'у найти правильное разбиение на страницы.
Определение команды \razdel можно дать, например, так:
\newcommand{\razdel}[1]{\par % завершить предыдущий абзац \pagebreak[2]\vspace{1cm plus 3mm minus .5mm} % см. ниже \refstepcounter{razdel}% новый номер раздела {\Large\rmfamily\bfseries\upshape % шрифт для заголовка \therazdel{} #1% заголовок \par % закончить заголовок }% завершить группу, внутри которой менялся шрифт \nopagebreak % чтобы не оторвать текст от % заголовка \vspace{2mm plus 1mm}% Промежуток между заголовком % и текстом }% конец макроопределения Пояснений тут требует команда \pagebreak[2]. Мы включили ее в макроопределение, чтобы поменьше разделов начиналось внизу страницы. В самом деле, команда \pagebreak[2] предлагает TeX'у начать в этом месте новую страницу; если так и будет сделано, то дополнительный вертикальный промежуток, созданный командой \vspace, пропадет, и заголовок раздела начнется с самого верха новой страницы; если же разрыва страницы все-таки не произойдет, то перед заголовком раздела будет вертикальный промежуток в один сантиметр (обладающий указанными в макроопределении растяжимостью и сжимаемостью).
Нам осталось только задать вид, в котором будут представляться на печати номера глав и разделов. Иными словами, надо переопределить должным образом команды \theglava и \therazdel (в момент создания счетчиков они, как мы помним, были автоматически определены таким образом, что \theglava и \therazdel — номера главы и раздела, набранные арабскими цифрами).Предположим, мы решили, что номера глав будут печататься римскими цифрами, а номер второго раздела четвертой главы будет иметь вид IV-2. Тогда требуемые переопределения таковы:
\renewcommand{\theglava}{\Roman{glava}} \renewcommand{\therazdel}{\theglava--\arabic{razdel}} Еще одно замечание: точки после номера главы мы включили в определение команды \glava, а не \theglava, чтобы можно было пользоваться автоматическими ссылками: если бы \theglava определялось как
\Roman{glava}. то исходный текст
в главе \ref{metka} мы пишем... дал бы на печати
в главе IV. мы пишем что нелепо.
По сравнению с макроопределениями, реально используемыми в стандартных классах LaTeX'а, мы многого не предусмотрели: не позаботились ни о колонтитулах, ни об автоматически генерируемом оглавлении, внешний вид заголовков оставляет желать лучшего и т.д. Прочитав лекцию 9, вы сможете усовершенствовать эти определения.
Отношение подчинения между счетчиками
Команда \z, как мы ее определили ранее, нумерует задачи автоматически, но при этом нумерация получается " сплошной". Часто, однако, требуется, чтобы в каждом разделе документа нумерация задач начиналась заново, так что шестая задача в разделе с номером 3 была озаглавлена Задача 3.6, а первая задача в разделе с номером 4 — Задача 4.1. Сейчас мы узнаем, как этого добиться.
Выше мы упоминали, что к моменту начала обработки LaTeX'ом нашего текста некоторые счетчики уже определены. В частности, это счетчики, содержащие номера текущих разделов документа. Их имена совпадают с именами команд, генерирующих эти разделы: chapter (если классом предусмотрено разбиение на главы), section, subsection и т.д. При каждом исполнении, например, команды \section значение счетчика section увеличивается на 1, и значение этого счетчика в каждый момент равно номеру текущего раздела. Поэтому, если в определении команды \z написать
\arabic{section}.\arabic{zadacha}.то перед номером задачи будет печататься номер текущего раздела и точка.
Но как же все-таки сделать, чтобы в каждом разделе нумерация задач начиналась заново? Можно, конечно, в начале каждого раздела присваивать счетчику zadacha значение

При этом счетчик zadacha будет подчинен счетчику section: всякий раз, когда значение счетчика section увеличивается на единицу командой \section, значение счетчика zadacha будет устанавливаться в нуль, и тем самым счет задач будет в каждом разделе начинаться заново. Одновременно надо в очередной раз исправить определение команды \z и написать
\newcommand{\z}{\par\addtocounter{zadacha}{1}% \textbf{Задача \arabic{section}.\arabic{zadacha}.} }При этом нумерация задач будет начинаться заново в каждом разделе, и вторая задача третьего раздела будет иметь номер 3.2.
Теперь сообщим точные правила создания счетчика, подчиненного другому счетчику. Они просты: команда \newcounter может принимать один необязательный аргумент (после обязательного) — имя того счетчика, которому будет подчинен определяемый нами счетчик.
Параметры со значением длины
Наряду со счетчиками — переменными с целочисленными значениями, — при создании собственных макроопределений возникает нужда и в переменных, значениями которых являются длины. Например, в предыдущем разделе мы, разрабатывая команду \razdel, в явном виде задали промежуток между заголовком раздела и остальным текстом. Если этот промежуток нам почему-либо захочется изменить, то придется снова залезать в определение команды \razdel. Было бы удобнее, если бы в нашем распоряжении был параметр под названием, скажем, \otstup, так что можно было бы в определении команды \razdel написать
\vspace{\otstup}и потом отдельно написать, допустим,
\otstup=1cm plus 3mm minus .5mmПравда, в богатом наборе TeX'овских и LaTeX'овских параметров требуемого нам параметра \otstup нет, но это не страшно, поскольку его можно создать. Для этого используется команда \newlength:
\newlength{\otstup}После того, как вы (допустим, в преамбуле) дали эту команду, будет определен новый параметр со значением длины; его можно будет обычным образом использовать в аргументах команд наподобие \vspace, и ему можно будет обычным образом присваивать значения.
Теперь — точные правила. Команда \newlength имеет один обязательный аргумент — имя команды, обозначающей определяемый вами параметр. Это имя должно подчиняться обычным правилам для TeX'овских команд (backslash, после которого следует либо одна не-буква, либо последовательность букв). Если это имя уже занято, LaTeX выдаст сообщение об ошибке. Определение нового параметра, совершаемое командой \newlength, является "глобальным": даже если эта команда была дана внутри группы, TeX будет помнить о существовании этого параметра и по выходе из группы. По этой причине разумное место для команды \newlength — преамбула.
Определенный нами параметр со значением длины приобретает такой же статус, как уже существующие TeX'овские и LaTeX'овские параметры (\parindent, \textwidth и другие). Рассмотрим, что можно делать с этими параметрами.
Во-первых, параметрам со значением длины можно присваивать значения.
Делается это точно так же, как это объяснялось ранее на примере параметра \parindent: для присваивания значения надо написать имя параметра, знак равенства, а после знака равенства — величину присваиваемой длины. Пробелы после указания единицы длины TeX'ом игнорируются (скорее всего, вы будете присваивать значения параметрам в преамбуле документа или между абзацами, где лишние пробелы никого не волнуют). Длина должна быть выражена в единицах, воспринимаемых TeX'ом. Даже если вы присваиваете нулевую длину, какая-то единица длины должна быть явно указана (например, 0pt). Кроме того, можно воспользоваться LaTeX'овской командой \setlength, имеющей два обязательных аргумента: первый — имя параметра, второй — значение длины, присваиваемое этому параметру. Таким образом, команды
\parindent=1.5em и
\setlength{\parindent}{1.5em} равносильны. Наконец, присваивания, сделанные внутри группы, забываются по выходе из этой группы.
В предыдущем абзаце мы умолчали об одной возможной неприятности. Дело в том, что если после команды присваивания, не использующей \setlength, следует (пусть даже после пробела) слово plus или minus, то TeX, скорее всего, выдаст сообщение об ошибке, поскольку решит, что длина должна иметь, помимо " естественного размера", еще и plus- или minus-компоненту. Если вы пишете текст на русском языке, вероятность такого стечения обстоятельств ничтожна, но тем не менее забывать о такой опасности не следует, особенно если команда присваивания входит в макроопределение: вы же не знаете заранее, в какое место может попасть новый макрос. Чтобы застраховаться от этой неприятности раз и навсегда, пользуйтесь командой \setlength, хоть это и длиннее.
Параметры со значением длины можно использовать всюду, где в аргументе LaTeX'овской команды требуется указать размер. Пусть, например, в преамбуле документа написано
\newlength{\primer} Тогда посмотрите на следующий пример:

Параметры со значением длины можно указывать с коэффициентом - положительной или отрицательной десятичной дробью (можно использовать как десятичную точку, так и десятичную запятую). Например, если значение параметра \primer равно


Параметры со значением длины (возможно, с числовыми коэффициентами) могут также стоять в правой части оператора присваивания (или во втором аргументе команды \setlength):
\primer=1.45\parindent \setlength{\primer}{.45\tabcolsep} Можно также прибавлять длину к значению параметра: если значение параметра \abcd равно

\addtolength{\abcd}{"$y$\verb"} где



\settowidth{"\textit{параметр}\verb"}{"\textit{текст}\verb"} которая присваивает параметру значение, равное ширине текста. Вот пример:

Существуют также команды \settoheight и \settodepth, аналогичные \settowidth. Команда \settoheight присваивает параметру значение, равное максимальному расстоянию, на которое текст возвышается над строкой (точнее, над ее базисной линией). \settodepth присваивает параметру значение, равное максимальному расстоянию, на которое текст опускается ниже базисной линии.
Ранее у нас шла речь о том, что некоторые используемые в TeX'е длины могут обладать растяжимостью или сжимаемостью. Параметрам, созданным с помощью команды \newlength, также можно присваивать значения, содержащие plus и/или minus -компоненту. Если, например, мы хотим, чтобы параметр \primer имел естественный размер


\setlength{\primer}{2cm plus 4mm minus 1pt}
Счетчики
Теперь мы научимся самостоятельно организовывать автоматическую нумерацию, подобно тому, как LaTeX автоматически нумерует главы, страницы, формулы и т.д. Для этого нам надо познакомиться с понятием счетчика. Счетчик — это специальная переменная, значение которой является целым числом. Ей можно присваивать различные значения, выводить значение счетчика на печать, а также организовывать с помощью счетчиков автоматическую генерацию ссылок. Рассмотрим последовательно, как все это делается.
Счетчики, которые уже определены
Мы уже мельком упоминали, что при начале работы LaTeX'а некоторые счетчики определены сразу. Например, это те счетчики, которые перечислены выше. Кроме того, заранее определен счетчик page, отвечающий за нумерацию страниц, а также счетчик footnote, ответственный за нумерацию сносок. Нумерацией плавающих иллюстраций и таблиц занимаются счетчики, называемые figure и table. В одном из разделов перечислены все эти заранее определенные счетчики и указано, каким счетчикам они подчинены (это иногда зависит от класса документа).
Для каждого из этих счетчиков вы имеете возможность переопределить соответствующую the - команду и тем самым изменить стиль оформления документа. Например, вы можете сделать так, чтобы главы нумеровались римскими цифрами:
\renewcommand{\thechapter}{\Roman{chapter}}Если вы хотите, чтоб сноски нумеровались не цифрами, а латинскими буквами, то можно в преамбуле написать:
\renewcommand{\thefootnote}{\alph{footnote}}Создание новых команд
Средства LaTeX'а, описываемые в этой лекции, позволяют сократить число нажатий на клавиши при наборе сложных текстов. Именно, мы расскажем, как создавать новые команды (или, если угодно, сокращенные обозначения), заменяющие собой длинные фрагменты из текста и TeX'овских команд. Официально такие новые команды называются макроопределениями, а в разговорной речи — макросами.
Создание счетчиков и простейшие операции с ними
Каждый LaTeX'овский счетчик имеет свое имя — последовательность букв (без знака \ ). Прописные и строчные буквы в именах счетчиков различаются; если в используемой вами русификации русские буквы нельзя употреблять в именах команд, то нельзя их употреблять и в именах счетчиков. Чтобы можно было работать со счетчиком, надо его создать командой \newcounter, имеющей один обязательный аргумент — имя, которое вы придумали для счетчика. Например, команда
\newcounter{abcd}создает новый счетчик с именем abcd. Если имя, которое вы придумали для счетчика, уже занято (так может случиться, даже если команда \newcounter в вашем тексте всего одна: некоторые счетчики в LaTeX'е уже определены в момент начала обработки вашего текста), то LaTeX создавать счетчик с таким именем откажется и выдаст сообщение об ошибке.
В отличие от многих других LaTeX'овских команд, команда для создания нового счетчика является "глобальной": даже если она давалась внутри группы, LaTeX не забудет о существовании определенного ею счетчика и после выхода из этой группы. Это отличает \newcounter от \newcommand и \renewcommand.
Что же можно делать со счетчиком? Во-первых, можно менять его численное значение (на программистском жаргоне: "присваивать счетчику различные значения"). При создании счетчика его значение устанавливается в

то после того, как TeX прочтет эту команду, значение счетчика abcd установится равным

Другой способ изменить значение счетчика — это прибавить к нему какое-то целое число. Для этого используется команда \addtocounter. Эта команда также имеет два обязательных аргумента: первый — имя счетчика, второй — число, которое прибавляется к счетчику.
Например, после выполнения команд
\setcounter{abcd}{100} \addtocounter{abcd}{-27} значением счетчика abcd будет число

Команды, изменяющие значение счетчика, также являются " глобальными": если с их помощью внутри группы значение счетчика было изменено, то по выходе из группы его прежнее значение не восстановится.
Перейдем к самому главному: как вывести значение счетчика на печать. Самый распространенный случай — печать значения счетчика обычными (" арабскими") цифрами. Для этого используется команда \arabic:
 | \setcounter{abcd}{40} Шел по улице отряд - \arabic{abcd} мальчиков подряд. |
Чтобы напечатать значение счетчика римскими цифрами, надо воспользоваться командой \Roman (если мы хотим, чтобы римские цифры записывались прописными латинскими буквами) или \roman (чтобы записать римскую цифру строчными латинскими буквами):
 | \setcounter{abcd}{14} Людовика \Roman{abcd} звали ``Король-Солнце''. |
Можно, наконец, напечатать букву латинского алфавита, порядковый номер которой равен значению счетчика. Для этого используются команды \alph(для печати строчной буквы) и \Alph(для печати прописной буквы):
 | \setcounter{abcd}{7} Наконец я узнаю, какая буква стоит в латинском алфавите на седьмом месте! Вот она: \alph{abcd}. |
В LaTeX'е отсутствует команда, позволяющая напечатать русскую букву с номером, равным значению счетчика. Средствами TeX'а такую команду нетрудно создать.
Наконец, можно напечатать один из девяти символов, используемых иногда в англоязычных странах для обозначения последовательных сносок (вместо цифр).
Для этого используется команда \fnsymbol, применять которую можно только внутри формул:
 | \setcounter{abcd}{0} Для сносок в Англии применяют такие символы: $\addtocounter{abcd}{1}\fnsymbol{abcd}$, $\addtocounter{abcd}{1}\fnsymbol{abcd}$, $\addtocounter{abcd}{1}\fnsymbol{abcd}$, а дальше попробуйте сами. |
В командах для изменения значений счетчиков можно вместо явного указания чисел использовать значения других счетчиков, для чего употребляется команда \value. Например, в результате выполнения команд
\newcounter{efgh} \setcounter{abcd}{10} \setcounter{efgh}{100} \addtocounter{efgh}{-\value{abcd}} значение счетчика efgh станет равно

\setcounter{efgh}{1000} \tolerance=\value{efgh} но большого смысла в таких трюках, как правило, нет.
Применим наши познания к делу. Ранее мы обещали вам так усовершенствовать макрос \z, начинающий новый абзац и печатающий жирным шрифтом слово "Задача", чтоб он еще и автоматически нумеровал эти задачи, так, что можно было бы просто писать в исходном тексте
\z Найти сумму... \z Решить уравнение... \z Поезд вышел из пункта А... и при этом знать, что номера LaTeX проставит сам. Теперь мы в состоянии решить эту проблему. Во-первых, для этого надо создать счетчик, значение которого в каждый момент будет равно номеру последней обработанной задачи; во-вторых, в определении команды \z надо предусмотреть, чтобы всякий раз значение этого счетчика увеличивалось на единицу, а затем печаталось в качестве номера задачи. В качестве имени счетчика выберем бесхитростное "zadacha":
\newcounter{zadacha} (напомним, что при выполнении этой команды счетчику zadacha будет присвоено значение

\newcommand{\z}{\par\addtocounter{zadacha}{1}% \textbf{Задача \arabic{zadacha}.} } Напомним, что команда \par означает "завершить предыдущий абзац, если он еще не был завершен"; без нее можно обойтись, если мы будем ставить команду \z только после пустой строки.Знак процента мы поставили, чтобы убрать лишний пробел, порождаемый концом строки. Теперь при первом исполнении команды \z значение счетчика zadacha станет равно


Бесконечно сжимаемые интервалы
Мы уже два раза упомянули про клей с бесконечной сжимаемостью. Настало время объяснить, какими командами его создавать. Из многих способов укажем один, наиболее часто встречающийся. Команда \hss вставляет в строку клей, естественный размер которого равен нулю, и который при этом обладает бесконечной растяжимостью (подобно \hfil) и бесконечной сжимаемостью. Типичное применение такого "бесконечно сжимаемого" клея — создавать блоки, ширина которых меньше реального размера текста, или блоки с наложением текстов. В самом деле, посмотрите на такой пример:

Если мы просим сделать ширину блока больше естественной, команда \hss действует так же, как и \hfil; когда мы создаем блок с естественной шириной, слова "Кот" и " Пес" стоят вплотную друг к другу (естественная ширина клея, созданного \hss, равна нулю). Интересные вещи начинаются, когда мы просим, чтобы ширина была


Еще один пример использования \hss: как создать блок, точка отсчета которого будет находиться в правом, а не левом конце текста (мы столкнулись с этой проблемой в лекции 5)? Ответ: надо сказать
\hbox to 0pt{\hss текст} и все будет в порядке. В самом деле, \ текст имеет ширину, отличную от нуля; чтобы блок имел в итоге нулевую ширину, приходится "уменьшать" тот интервал, где стоит \hss; так как интервал уже нулевой, то это уменьшение сводится к тому, что текст сдвигается влево до тех пор, пока расстояние между его концом и точкой отсчета не станет равным нулю - а это и означает, что правый конец текста стал его точкой отсчета. В лекции 5 мы сказали, что эта проблема решается с помощью TeX'овской команды \llap, а теперь мы видим, как ее можно определить:
\newcommand{\llap}[1]{\hbox to 0pt{\hss #1}} Кстати говоря, именно так она и определяется.
А если сказать
\hbox to 0pt{текст \hss} то что, спрашивается, будет? Ответ: на сей раз будет уменьшаться интервал после текста; стало быть, сам текст никуда не сдвинется, но после него будет сделан такой "отрицательный пробел", чтобы суммарная ширина равнялась нулю. Иными словами, TeX будет просто считать, что ширина блока равняется нулю - мы обманули TeX, убедив его, что наш текст не занимает места по горизонтали! Для такого обмана (к нему приходится прибегать нередко) предусмотрена специальная TeX'овская команда \rlap, определяемая так:
\newcommand{\rlap}[1]{\hbox to 0pt{#1\hss}} Все это также напоминает ситуацию с командой \lefteqn — и напоминает не случайно, поскольку эта команда определяется фактически так:
\newcommand{\lefteqn}[1]{\rlap{$\displaystyle #1$\hss}}
Блоки из абзацев
Если необходимо создать блок, в котором размещается сверстанный TeX'ом абзац текста, то можно воспользоваться командой \parbox. У этой команды два обязательных аргумента: первый — длина строк в получаемом абзаце, второй — собственно текст. Например, такой текст
 | В строку\qquad \parbox{4cm}{вставили целый абзац текста, сверстанного по всем TeX'овским правилам. После этого продолжается}\qquad прерванная строка. |
Как видите, базисная линия блока, создаваемого командой \parbox, находится в точности посредине текста. Поэтому команду \parbox удобно использовать для включения больших фрагментов текста в математические формулы. Например, формула

получается из такого исходного текста:
$$ \int_a^b f'(x)\,dx=f(b)-f(a)\qquad \parbox{4cm}{для всех функций f, производная которых интегрируема по Риману} $$Если дать команду \parbox с необязательным аргументом} с необязательным аргументом, то создаваемый ею блок можно расположить относительно строки и по-иному: чтобы вровень с остальной строкой шла самая верхняя строка абзаца (для этого нужен аргумент t) или самая нижняя (аргумент b); можно также указать аргумент c — тогда блок будет расположен по центру, так же, как если бы необязательного аргумента вообще не было. Необязательный аргумент у этой команды должен идти перед обязательными.
Во втором обязательном аргументе команды \parbox, задающем текст, может присутствовать всё то же, что в обычном тексте, в том числе команды для вертикальных пробелов наподобие \vspace, пустые строки, разделяющие абзацы, выключные формулы и т.п. Абзацы, создаваемые командой \parbox, по умолчанию делаются без абзацного отступа и в режиме \sloppy. Если вы хотите чего-то другого, можно прямо внутри аргумента команды \parbox установить нужное вам значение абзацного отступа, параметра \tolerance и т.п.
Можно также указать LaTeX'у высоту, которую должен иметь блок, полученный в результате применения команды \parbox. Для этого используется второй необязательный аргумент, идущий непосредственно после первого.
Наряду с явным указанием размера, можно воспользоваться командой \height, обозначающей " естественную" высоту текста, а также командой \totalheight (высота плюс глубина).
Наконец, в команде \parbox можно указать, как именно должен быть расположен текст внутри блока. Для этого используется третий необязательный аргумент, следующий непосредственно после второго. Этот аргумент — буква t, b, c или s. Буква t означает " сверху", b — "снизу", c — "по центру". Если третий необязательный аргумент не указан, то по умолчанию считается, что он совпадает с первым. Если же третьим необязательным аргументом является s, это означает, что текст будет растянут или ужат в соответствии с размером, указанным во втором необязательном аргументе. Если вы не позаботитесь о специальных командах, обеспечивающих такую растяжимость или сжимаемость, то получите сообщение об Overfullе или Underfullе.
В следующем примере блоки, созданные командой \parbox, для наглядности взяты в рамку (с помощью \fbox):

\fbox{% \parbox[b][1.3\height]{2cm}{% Мы едем, едем, едем в далекие края.}}\qquad \fbox{% \parbox[t][1.3\height]{2cm}{% Мы едем, едем, едем в далекие края.}} Команды \height и \totalheight, так же как и \depth, можно использовать только в необязательном аргументе команды \parbox (а также \framebox или \makebox).
Наряду с \parbox, существует еще один способ создать блок из абзацев. Именно, существует окружение {minipage} (" министраница"), генерирующее блок из текста, расположенного внутри этого окружения; блок состоит из абзацев, ширина которых задается в обязательном аргументе окружения {minipage} (так же, как в команде \parbox); перед обязательным аргументом этого окружения может стоять необязательный: буква t, b или c, причем смысл этого аргумента опять-таки такой же, как в команде \parbox. Основное отличие minipage от \parbox в том, что к тексту внутри этого окружения можно делать сноски с помощью команды \footnote, причем текст сноски появляется не внизу страницы, а внизу блока, генерируемого окружением minipage.При наборе книги, которую вы читаете, это окружение использовалось для печати примеров.
Блоки из строки
С одной командой для генерации блоков мы уже знакомы: это команда \mbox. Эта команда создает блок из текста, набираемого в одну строку. Полученный блок рассматривается TeX'ом как одна буква:
 | Проказница мартышка, \mbox{осел, козел} и косолапый мишка\ldots |
В этом примере TeX никогда не разорвет строку между словами "осел" и "козел" и никогда не сделает переносов в этих словах: при верстке абзаца TeX имеет дело не с этими словами по отдельности, а только с блоком, в который входят они оба вместе с пробелом между ними. По той же причине TeX не сможет растянуть или сжать пробел между словами "осел" и "козел" для выравнивания строк в абзаце.
Теперь, когда мы знаем, что такое TeX'овские блоки, можно признаться, что окружения {picture},{tabular} и {array} тоже генерируют блоки, и именно поэтому создаваемый ими текст воспринимается TeX'ом как одна большая буква.
В аргументе команды \mbox может присутствовать все то же, что может быть в обычном тексте в пределах одной строки: математические формулы, команды смены шрифта или присваивания значений каким-то параметрам, команды для генерации блоков (например, тот же \mbox, или даже окружения {picture} или {array}) и т.д. Запрещены в аргументе команды \mbox пустые строки или команды \par, выключные математические формулы, окружения, определяющие абзацы специального вида (скажем, {itemize} или {center}), команда \\ и тому подобные вещи, "не вписывающиеся в строку". Если в аргументе команды \mbox происходит смена шрифта, изменение каких-то параметров или определение команд, то по выходе из блока все эти изменения забываются, поскольку фигурные скобки, ограничивающие аргумент команды \mbox, ограничивают также и группу (" глобальные" команды вроде \setcounter сохраняют свое действие и по выходе из блока).
Блок, создаваемый командой \mbox, имеет ширину, равную " естественной" длине строки текста, являющегося его аргументом. Можно также создать блок из строки текста, ширина которого отлична от ее естественной длины.
Для этого используется команда \makebox. Эта команда имеет один обязательный аргумент, имеющий такой же смысл, как аргумент команды \mbox, и, кроме того, необязательный аргумент — ширину блока, порождаемого командой:
 | Туда \makebox[5em]{и} обратно. |

Для ясности мы использовали в этом примере крупный шрифт. А вот как такой "выпирающий за края" блок взаимодействует с окружающим текстом:
 | текст\makebox[1.5em]{123456}текст |
 | \parindent=0pt \makebox[10em][r]{текст}\\ \makebox[10em][r]{екст}\\ \makebox[10em][r]{кст}\\ \makebox[10em][c]{текст}\\ \makebox[10em][l]{текст} |
Кстати, обратите внимание, что у нас получилась верстка с выравниванием без помощи таких вещей, как tabbing или tabular.
У команды \makebox значение ширины блока можно установить равным нулю. Если при этом присутствует необязательный аргумент l, то получится блок нулевой ширины, а текст будет выходить за его пределы вправо (и, стало быть, наложится на последующий текст в строке, если таковой присутствует); если присутствует необязательный аргумент r, то текст будет выходить влево за пределы блока (и тем самым накладываться на предшествующий текст):
 | текст\makebox[0pt][l]{???}текст\\ текст\makebox[0pt][r]{???}текст\\ |
До сих пор мы задавали ширину блока в команде \mbox в явном виде. Можно, кроме того, выразить эту ширину через " естественную" ширину текста. Для этого служит команда \width. Вот, например, как сделать, чтобы чтобы ширина блока, получаемого с помощью \makebox, была на 30% больше естественной:
 | \makebox{скоросшиватель}\\[2pt] \makebox[1.3\width][r]{скоросшиватель} |
Блоковые переменные
В тех случаях, когда один и тот же фрагмент текста (например, фрагмент псевдорисунка, являющийся аргументом команды \multiput) используется многократно, бывает полезно сверстать этот фрагмент раз и навсегда, а затем просто повторять его: это сэкономит как количество нажатий на клавиши, так и машинное время. Использование макроопределения в данном случае времени не сэкономит: если мы напишем, например,
\newcommand{\abcd}{\parbox{6cm}% {Когда в товарищах согласья нет, на лад их дело не пойдет, и выйдет из него не дело — только м\'ука.}}то при каждой обработке команды \abcd это макроопределение будет заново развертываться, и TeX будет заново находить переносы и места разрыва строк в одном и том же отрывке из " Лебедя, рака и щуки". Чтобы не заставлять TeX много раз повторять идентичные операции по верстке текста, надо сделать так. Во-первых, определим "блоковую переменную", которая будет хранить сверстанный фрагмент текста. Это делается с помощью команды \newsavebox. Единственный аргумент этой команды - имя новой блоковой переменной, которое должно удовлетворять тем же условиям, что любые имена TeX'овских команд: либо backslash с одной не-буквой, либо backslash с последовательностью букв. Имя новой блоковой переменной не должно совпадать с именем уже существующей команды или переменной длины (если вы попытаетесь нарушить это правило, LaTeX выдаст сообщение об ошибке). Во-вторых, присвоим нашей блоковой переменной значение — блок, и будем в дальнейшем этот блок использовать.
Давайте приведем пример того, как можно этим пользоваться. Выше мы приводили пример псевдорисунка — наклонной решетки, и там же мы отметили, что экономнее было бы создать наклонный отрезок раз и навсегда, а затем только повторять его. Теперь мы можем объяснить, как это сделать. Создадим блоковую переменную под названием \blok, написав в преамбуле следующее:
\newsavebox{\blok}Теперь сверстаем тот текст, который будет храниться в нашей блоковой переменной, и запишем его в эту переменную.
Для этих целей используется команда \sbox с двумя обязательными аргументами: первый — имя блоковой переменной, второй — текст, который в нее записывается. Итак:
\sbox{\blok}{\line(1,5){10}} А теперь можно воспользоваться нашей блоковой переменной. Чтобы напечатать содержимое блоковой переменной, используется команда \usebox с одним обязательным аргументом — именем переменной. В нашем случае мы используем блоковую переменную в аргументе команды \multiput:

\begin{picture}(100,50) \multiput(0,0)(10,0){10}% {\usebox{\blok}} \multiput(0,0)(2,10){6}% {\line(1,0){90}} \end{picture} Можно было бы сделать аналогичный трюк и с горизонтальными линейками решетки, но большой экономии это не даст: горизонтальные и вертикальные линейки на псевдорисунках LaTeX не собирает из отдельных символов, а создает "в один присест" с помощью команд \hrule и \vrule, что и так достаточно быстро.
Текст, присутствующий в аргументе команды \sbox, будет сверстан в виде блока так, как если бы этот текст был передан в качестве аргумента команде \hbox или \mbox. Тем самым в аргументе \sbox может быть все то же, что может присутствовать в аргументе \hbox или \mbox. Если команда \sbox была дана внутри группы, то по выходе из этой группы содержимое блоковой переменной забудется.
Наряду с командой \sbox есть еще и команда \savebox, относящаяся к ней примерно так же, как \makebox относится к \mbox: между первым и вторым обязательным аргументами команды \savebox могут присутствовать необязательные аргументы, имеющие тот же смысл и записывающиеся так же, как необязательные аргументы команды \makebox. Например,
\savebox{\пример}[4cm][r]{Слово} даст тот же результат, что и
\sbox{\пример}{\makebox[4cm][r]{Слово}} Наряду с LaTeX'овской командой \usebox есть похожая на нее, но не идентичная, TeX'овская команда \copy. Используется она так:
 | \sbox{\blok}{Рак} Однажды Лебедь, \copy\blok{} и Щука\ldots |
Эту разницу следует иметь в виду, когда вы работаете с командой \leaders: выгоднее сверстать блок один раз и записать его в блоковую переменную, а затем в команде \leaders писать просто \copy. Пример:
 | \savebox{\blok}[1cm]{$*$} \hbox to \textwidth {\leaders\copy\blok\hfil} |
Для тех, кто будет читать следующую лекцию, скажем еще об одной конструкции, связанной с блоковыми переменными. Именно, если \blok — блоковая переменная, то можно " измерить" ширину, высоту и глубину блока, записанного в этой переменной, с помощью TeX'овских команд \wd, \ht и \dp. Точнее говоря, сочетания \wd\blok, \ht\blok и \dp\blok можно использовать в точности так же, как TeX'овские параметры со значением длины, значения которых равны ширине, высоте и глубине блока:
 | \sbox{\blok}{12345}\copy\blok\\ \hbox to \wd\blok{\hfil 345}\\ \hbox to \wd\blok{\hfil 45} |
 |
 |
 |
2) Пустых строк, однако, быть не должно.
3) Если мы заставим такую пружину растянуться или сжаться больше, чем сказано, то получим сообщение "Underfull \hbox" или "Overfull \hbox"; см.\ ниже.

Еще раз о линейках
В аргументе команды \hbox может присутствовать и TeX'овская команда \vrule. Ее ценность в том, что она автоматически создает линейку, высота и глубина которой равна высоте и глубине объемлющего блока (ширина этой линейки будет по умолчанию равна


Предыдущий абзац в исходном тексте выглядел так:
\begin{flushleft} \hbox{% \vrule\hspace{.5em}\parbox{.9\textwidth}% {Иногда используется следующий способ выделения текста: абзац набирается с некоторым отступом от левого поля, а слева от него, вровень с левым полем, печатается вертикальная линейка.}} \end{flushleft}Этот текст нуждается в некоторых пояснениях. Во-первых, в последней строке первая из фигурных скобок закрывает аргумент команды \parbox, а вторая - \hbox. Во-вторых, мы воспользовались окружением \flushleft, чтобы LaTeX сам позаботился о разумных отступах до и после абзаца. Параметр \textwidth означает, как мы помним, ширину страницы. Теперь рассмотрим, что присутствует внутри \hbox. Сначала там идет линейка, затем отступ на

Обратите еще внимание на знак процента после \hbox — без него получилось бы, что аргумент команды \hbox начинается с пробела, соответственно и линейка начиналась бы не с начала, а после пробела .
На самом деле в предыдущем примере было бы лучше, если бы правый край выделенного абзаца шел вровень с правым краем остального текста. Чтобы добиться этого, надо первый аргумент команды \parbox не взять с потолка, а вычислить. Для этого нам понадобятся переменные со значением длины. Предполагая, что мы определили с помощью \newlength переменные \shirina и \raznost, сделаем вот что:
\begin{flushleft} \shirina=\textwidth \settowidth{\raznost}{\vrule\hspace{.5em}} \addtolength{\shirina}{-\raznost} \noindent\hbox{% \vrule\hspace{.5em}\parbox{\shirina}% {Иногда используется ... ... линейка.}} \end{flushleft} Мы воспользовались командой \settowidth, чтобы найти размер, который занимает линейка вместе с пробелом. Кстати, если просто написать \hbox{\vrule\hspace{.5em}}, то на печати мы ничего не увидим (внутри \hbox'а никакого текста нет, так что высота и глубина линейки равна нулю и она тем самым невидима); однако же эта команда создаст пробел, величина которого равна 0.4pt плюс 0.5em. Заключительное замечание: поскольку {flushright}, как и всякое окружение, ограничивает группу, все наши манипуляции с параметрами \shirina и "\raznost" забудутся по выходе из этого окружения.
Клей
Выше мы рассмотрели команды \hfil и \hfill, которые действуют подобно вставленным в строку пружинам. Можно вставлять в строку пружины с самыми разнообразными свойствами, указав LaTeX'овской команде \hspace аргумент, содержащий plus- или minus-компоненту (в разд.3.9.4 мы упоминали об этой возможности, но в тот момент у нас еще не было серьезных примеров). Именно, если вы скажете
\hspace{"$x$ plus $y$ minus $z$"}где













Опишем более точно, как именно растягивается или сжимается клей при выполнении команды \hbox to ... Для простоты предположим дополнительно, что plus- и minus- компоненты клея всюду неотрицательны и что в строке отсутствует клей с бесконечной растяжимостью или сжимаемостью (в частности, в строке нет \hfil'ов или \hfill'ов; про клей с бесконечной сжимаемостью речь пойдет ниже).
В этом случае TeX вычисляет "естественную ширину" блока, складывающуюся из ширин составляющих его элементов и естественных размеров клея, и сравнивает ее с требуемой шириной блока, указанной в команде \hbox после ключевого слова to. Если эти две ширины совпали, то все пробелы будут иметь естественный размер. Если требуемая ширина больше естественной, то TeX вычисляет, насколько больше, после чего "разверстывает" эту добавку между всеми пробелами пропорционально величинам plus - компонент клея в этих пробелах.
Вот пример. Предположим, мы создаем блок с помощью команды
\hbox to $a$ {А\hspace{0pt plus 2em}% Б\hspace{1cm plus 1em minus 2mm}В} где величина




В приведенном примере оба пробела в блоке были созданы вручную командой \hspace; если же в аргументе команды \hbox присутствуют пробелы, то следует учесть, что эти пробелы также, как мы объясняли ранее, обладают растяжимостью и сжимаемостью, которая также берется в расчет.
В случае, когда пробелы надо растягивать и требуемое растяжение блока больше, чем сумма plus - компонент всех элементов клея, на экран и в log -файл выдается знакомое вам сообщение Underfull \hbox; если пробелы надо уменьшать и величина, на которую надо уменьшить ширину блока, меньше, чем сумма minus - компонент всех элементов клея, то выдается не менее знакомое сообщение Overfull \hbox.
Все сказанное относилось к случаю, когда бесконечно растяжимого клея в аргументе команды \hbox нет.
Если же таковой присутствует (например, есть команда \hfil) и пробелы надо растягивать, то растяжимость клея с конечными значениями plus -компонент утрачивается: соответствующие интервалы будут иметь естественный размер (что бы ни было написано в аргументе команды \hspace после plus), а все растяжения будут происходить только за счет команд \hfil. При этом сообщение об Underfull'е выдаваться не будет, как бы ни растянулись пробелы. Аналогично, если пробелы надо ужимать и присутствует клей с бесконечной сжимаемостью, все уменьшения пробелов произойдут только за его счет и никогда не будет выдано сообщения об Overfull'е.
Если в аргументе команды \hbox присутствуют команды \hfil и \hfill совместно, то при необходимости растягивать пробелы учитывается только \hfill, в то время как "в бесконечное число раз менее растяжимый" \hfil в расчет не берется (не говоря уж о клее с конечной растяжимостью):
 | \hbox to 4cm{\hfil Блоки и клей\hfil} \hbox to 4cm{\hfil Блоки и клей\hfill} \hbox to 4cm{\hfill Блоки и клей\hfill} |
Команда \hbox
Возможности, предоставляемые LaTeX'ом для генерации блоков, достаточны для простых приложений, но в более серьезных случаях их не хватает. В этом и следующем разделах мы рассмотрим более гибкие средства, предоставляемые для этой цели непосредственно языком TeX и макропакетом Plain - TeX. Мы не будем пытаться описать все TeX'овские команды для генерации блоков (книгу [2] ничто заменить не может), но сообщим тот минимум сведений, который необходим для модификации LaTeX'овского стандартного оформления, о чем пойдет речь в следующей лекции. Подчеркнем, что всеми описываемыми в этом и следующем разделах TeX'овскими средствами можно пользоваться в LaTeX'овских исходных текстах.
Прежде всего давайте вспомним, что в каждый момент трансляции исходного текста TeX находится в одном из трех следующих режимов: горизонтальном (в процессе верстки абзаца), вертикальном (между абзацами), или математическом (в процессе набора математической формулы); при появлении первой же буквы или LaTeX'овской команды для генерации блока или линейки (к таковым относятся \mbox, \makebox, \fbox, \framebox, окружения {array}, {tabular} или {picture}, а также команда \rule1)) TeX из вертикального режима выходит и начинает очередной абзац.
Одна из основных TeX'овских команд для генерации блоков называется \hbox. В своем простейшем виде она полностью аналогична LaTeX'овской команде \mbox, с одним важным отличием: в вертикальном режиме команда \hbox не начинает нового абзаца, а только добавляет сгенерированный ею блок (т. е.\ фактически строку) к уже сверстанной части страницы. Внутри абзаца (в горизонтальном режиме) команда \hbox действует точно так же, как и \mbox. Вот пример:

Сравните с тем, что было бы при использовании LaTeX'овской команды \mbox вместо \hbox:

Команда \vbox
Теперь рассмотрим вторую основную команду TeX'а для генерации блоков — команду \vbox. Эта команда создает блок, обрабатывая текст в вертикальном режиме. Вот первый пример:

Получаемый блок имеет вид:
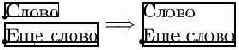
Как видите, блоки, создаваемые \hbox, ставятся один под другим таким образом, чтобы их точки отсчета лежали на одной вертикальной прямой.
Прежде чем идти дальше, обсудим, что может содержаться в аргументе команды \vbox. Там могут присутствовать любые TeX'овские команды, допустимые между абзацами (т.е. в вертикальном режиме): команды \vspace, команды смены шрифта, присваивания значений различным параметрам, команды \newcommand и \renewcommand и т.п. Что же касается команд, которым соответствует что-либо на печати, то будем считать, что из них в аргументе \vbox возможны только TeX'овские команды \hbox, \vbox и \hrule, а также \copy, о которой речь пойдет позже. В частности, недопустим ни текст, ни LaTeX'овские команды \mbox, \parbox, \rule и т.п. Если вам требуется воспользоваться возможностями таких команд, "прячьте" их в \hbox, например, так:
\hbox{\raisebox{1pt}[2em][3em]{...}}На самом деле в аргументе команды \vbox может находиться и обычный текст; при появлении первой же буквы или, скажем, команды \mbox или другой команды LaTeX'а для генерации блоков TeX переходит в горизонтальный режим, который продолжается до команды, завершающей абзац (\par или пустой строки). Мы не будем вдаваться в детали; для тех приложений, которые мы имеем в виду, достаточно использовать команду \vbox так, как было предписано выше.
Когда TeX при выполнении команды \vbox составляет блоки друг с другом, он располагает их так, чтобы их базисные линии были, по возможности, на равных расстояниях друг от друга, так что обычно между блоками будет присутствовать дополнительный пробел. С другой стороны, линейки, созданные командой \hrule, приставляются к блокам без дополнительного пробела. Чтобы при этом линейка не оказалась вплотную к тексту, удобно в соответствующий блок вставить \strut.
Следующий пример призван пояснить сказанное:

Неудачно:\\ \vbox{\hbox{Два слова} \hrule} Лучше так:\\ \vbox{\hbox{\strut Два слова} \hrule} Как обычно, \ vbox посреди абзаца ведет себя просто как большая буква. Обратите также внимание, что мы не пытались убрать лишний пробел между \hbox и \hrule: в вертикальном режиме пробелы никакого влияния на текст не оказывают.
Вот еще пример, когда с помощью комбинации блоков и линеек текст берется в рамку:

\vbox{\hrule \hbox{\vrule\,\strut Текст в рамке\,\vrule} \hrule} По-прежнему мы используем \strut, чтобы горизонтальные линейки не подходили слишком близко к тексту (и \ для той же цели по горизонтали).
Лидеры
В оглавлении к этой книге (и ко многим другим тоже) место между названием раздела и номером страницы заполняется рядом из точек. Это можно сделать с помощью LaTeX'овской команда \dotfill. Она работает так же, как и \hfill, с той разницей, что пробел, образующийся в результате действия этой команды, заполняется точками:
 | \hbox to 3cm{А\dotfill Б} |
Кроме этого, есть LaTeX'овская команда \hrulefill, которая также действует аналогично команде \hfill и при этом заполняет пробел линейкой:

В TeXнической терминологии такие заполнители называют лидерами (leaders).
На самом деле можно заполнить пробел не только точками или линейкой, но и любым повторяющимся текстом. Вот как это делается. Пусть мы хотим заполнить пробел повторяющимися твердыми знаками. Тогда можно написать так:
 | \hbox to 5cm{1\leaders \hbox{Ъ}\hfil 2} |
Если бы мы хотели, чтоб буквы Ъ шли не вплотную, можно было бы, например, вместо "Ъ" написать так:
\hbox to 2em{\hfil Ъ\hfil}В общем случае применяйте команду \leaders так:
\leaders $\langle$ \textit{блок}$\rangle$ $\langle\mbox{\cs(hfil) \textit{или} \cs(hfill)}\rangle$Здесь

Между командой для генерации блока и командой \hfil или \hfill может быть пробел (например, конец строки). Команда \leaders работает так: выделяется столько свободного места, сколько получилось бы, если бы стояло просто \hfil или \hfill, а затем это место заполняется идущими вплотную друг к другу копиями

С помощью команды \leaders можно также изменить толщину линейки, заполняющей свободное место. Именно, команда \hrulefill является по существу сокращением от
\leaders\hrule\hfillЕсли же мы скажем, например,
\leaders\hrule height 1pt \hfillто линейка будет иметь толщину 1 пункт, вместо принятых по умолчанию 0.4 пункта. Можно также написать \hfil вместо \hfill, с очевидными последствиями.
Растяжимые интервалы
До сих пор шла речь о важных, но непринципиальных различиях между TeX'овским \hbox и LaTeX'овским \mbox. Теперь поговорим о дополнительных возможностях, предоставляемых TeX'овской командой.
Команда \hbox "в чистом виде" создает блок, ширина которого равна естественной длине текста, являющегося ее аргументом. Кроме этого, она может создавать блоки любой заданной ширины. Для этого нужно сказать
\hbox to {ширина}{текст}Здесь {ширина}должна быть выражена в воспринимаемых TeX'ом единицах длины: это может быть, например, 20pt, или 2.3cm, или, например, 0.12\textwidth - параметр со значением длины (возможно, с коэффициентом) тоже годится. Между to и обозначением ширины, а также между обозначением ширины и открывающей фигурной скобкой могут быть пробелы - TeX их проигнорирует2). Наконец, отсутствие backslash в слове to не является опечаткой: это не команда, а одно из "ключевых слов" TeX'а (подобно ключевым словам plus и minus, с которыми мы вскоре снова встретимся, или width и height, с которыми мы уже встречались в разделе, посвященном линейкам). Давайте опробуем эту новую возможность команды \hbox:
 | \hbox to 3cm {Два слова} |
Если вы опробовали этот пример на вашем компьютере, то заметили, что на экране появилось сообщение
Underfull \hboxДело в том, что пробел между словами "Два" и " слова" не может растянуться настолько, чтобы наш блок имел ширину три сантиметра; в ситуациях, когда пробел насильно заставляют растянуться больше, чем положено, возникает сообщение об Underfull'е, как это было объяснено в разд. 3.6.6.
Можно, однако, заставить TeX создать блок требуемой ширины " без скандала". Для этого в том промежутке, который мы хотим растянуть, надо поставить команду \hfil:
 | \hbox {Два слова}\\ \hbox {Два \hfil слова}\\ \hbox to 2cm {Два \hfil слова}\\ \hbox to 3cm {Два \hfil слова}\\ \hbox to 4cm {Два \hfil слова} |
Если мы не указываем явно ширину блока, а предоставляем TeX'у создать блок "естественной" ширины, то команда \hfil никакого действия не оказывает; если промежуток для достижения требуемой ширины надо растянуть, то растяжение на требуемое расстояние будет проведено в том месте, где стоит команда \hfil.
Если в аргументе команды \ hbox присутствует не одна команда \hfil, а несколько, то растяжение произойдет на месте каждой из этих команд, причем размер этого растяжения будет распределен между командами \hfil равномерно: если необходимо превысить естественную ширину блока на


 | \hbox to 4cm{Раз \hfil два \hfil три} |

\hbox to 0.7\textwidth {Слева\hfil} \hbox to 0.7\textwidth {\hfil Справа} \hbox to 0.7\textwidth {\hfil В центре\hfil} Можно считать, что на месте каждого \hfil в строку вставляется пружина; все эти пружины имеют одинаковую жесткость, в свободном состоянии все они имеют нулевую ширину, и все эти пружины могут сколь угодно широко растягиваться.
Наряду с \hfil существует команда \hfill, также задающая бесконечно растяжимые пробелы, причем эта растяжимость "в бесконечное число раз больше", чем у пробелов, задаваемых \hfil. Если в аргументе команды \hbox присутствуют \hfil и \hfill совместно, то все растяжения происходят только за счет "более растяжимых" \hfill:
 | \hbox to 4cm{\hfil Слово\hfil}\\ \hbox to 4cm{\hfill Слово\hfil}\\ \hbox to 4cm{\hfil Слово\hfill} |
Сдвиги относительно базисной линии
Когда при исполнении команды \makebox или \mbox TeX создает блок из меньших блоков (каждая буква, как мы помним, - это блок, из букв составляются слова - тоже блоки; наконец, блоки могут быть заданы в явном виде, в частности, командой \mbox), то блоки эти размещаются в строке таким образом, что все их точки отсчета расположены на одной высоте (иными словами, их базисные линии продолжают одна другую). Можно, однако, сдвинуть блок по вертикали относительно базисной линии. Для этого удобно воспользоваться LaTeX'овской командой \raisebox. Эта команда требует двух обязательных аргументов. Первый из них - расстояние, на которое сдвигается по вертикали фрагмент текста, второй - сам этот фрагмент текста. Пример:
 | Слово \raisebox{2pt}{подскочило} в строке. |
Текст, расположенный во втором обязательном аргументе этой команды, должен удовлетворять тем же требованиям, что и аргумент команды \mbox: в нем могут быть самые разные TeX'овские команды, при условии, что среди них не будет команд типа пустой строки, \par, \\ и тому подобных, которые "не укладываются в строку" (зато в этом тексте, как водится, могут присутствовать любые команды, порождающие блоки, в частности, например, \parbox, а уж в ее аргументе оставляйте пустых строк, сколько душе угодно). Если первый обязательный аргумент команды \raisebox отрицателен, то текст будет, естественно, не поднят, а опущен. Вот, например, как можно определить команду \tex, печатающую эмблему TeX'а:
\newcommand{\TeX}{T\nolinebreak\hspace{-.1667em}\raisebox {-.5ex}{E}\nolinebreak\hspace{-.125em}X}Тут же мы видим и примеры использования отрицательных промежутков для того, чтобы буквы сблизились. Команды \nolinebreak нужны, чтобы не случилось разрыва строки посередине эмблемы.
На самом деле команда \TeX определяется более экономным способом, который требует меньше машинного времени и памяти, но использует не рассматриваемые нами средства TeX'а. Время от времени мы будем приводить определения команд "в переводе с TeX'а на LaTeX".
Кроме вертикального сдвига блоков, команда \raisebox может делать еще одно полезное дело: с ее помощью можно обмануть TeX, заставив его считать, что блок, полученный после сдвига, имеет любую заданную нами высоту и глубину, независимо от того, сколько места реально занимает текст. Именно, эта команда может принимать, наряду с обязательными, необязательные аргументы. Между двумя обязательными аргументами можно указать необязательный аргумент — высоту, которую, по мнению TeX'а, должен иметь сдвинутый блок. Кроме того, после первого необязательного аргумента может стоять второй — глубина, которую, по мнению TeX'а, будет иметь сдвинутый блок. Вот пример:
 | Строка.\\ Вторая \raisebox{7pt}[1pt][10pt]{Ы}\\ Третья строка. |
Иногда разумно использовать команду \raisebox даже с нулевым обязательным аргументом, только для того, чтобы менять (в глазах TeX'а) высоту и/или глубину блока, не сдвигая его относительно базисной линии. В лекции 9 мы увидим пример такого использования этой команды.
Текст состоит из блоков
Мы уже отмечали, что в процессе набора TeX не принимает во внимание, как буквы будут выглядеть на печати, а лишь учитывает, сколько места надо отвести на каждый символ. Давайте обсудим этот процесс подробнее.
С точки зрения TeX'а, каждая буква представляет собой блок (английский термин: box), т.е. прямоугольник с выделенной точкой отсчета; горизонтальная прямая, проходящая через точку отсчета, называется базисной линией (английский термин: baseline). Блок характеризуется тремя размерами: шириной, высотой и глубиной. См. рисунок, на котором также изображен блок, соответствующий букве у.
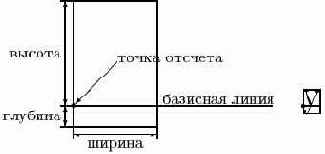
Когда из букв составляются слова (а из слов — строки), блоки, соответствующие отдельным буквам, ставятся рядом так, чтобы их базисные линии были продолжением друг друга. Каждая строка также становится блоком, точка отсчета которого совпадает с точкой отсчета первого из составляющих ее блоков:

Страницы - это тоже блоки, составленные из блоков, соответствующих строкам. Эти блоки ставятся таким образом, чтобы точки отсчета были одна над другой, после чего в качестве точки отсчета и базисной линии полученного блока берутся точка отсчета и базисная линия последнего из добавляемых блоков:

В приведенных выше примерах мы сталкивались с блоками, которые TeX создает автоматически; в настоящей лекции пойдет речь о командах, предназначенных для создания блоков вручную. Сначала мы расскажем, какие средства для этого предоставляет нам LaTeX, а затем рассмотрим некоторые TeX'овские команды, дающие дополнительные возможности.
Текст в рамке; комбинации блоков
В лекции 3 мы уже упоминали про команду \fbox, берущую в рамку фрагмент текста, помещающегося в строку. Наряду с ней есть и команда \framebox, относящаяся к ней так же, как \makebox относится к \mbox: она берет текст в рамку заданного размера, причем текст внутри этой рамки либо центрирует (если необязательного аргумента нет или же задан необязательный аргумент c), либо прижимает к правому или левому краю рамки (если задан необязательный аргумент r или l). Смысл и расположение обязательных и необязательных аргументов у команды \framebox такой же, как и у команды \makebox.
Точнее говоря, первый обязательный аргумент команды \framebox задает не ширину рамки, а ширину текста, помещаемого в эту рамку. Сама же рамка отделена от текста пробелом ширины \fboxsep; толщина линий в рамке равна \fboxrule. Обоим этим параметрам можно обычным образом присваивать новые значения.
Коль скоро каждый блок, создаваемый LaTeX'овскими командами, рассматривается TeX'ом просто как большая буква, возможны любые, сколь угодно причудливые, комбинации таких "букв". Пусть, например, нам надо взять в рамку абзац текста шириной


Просто поместить этот текст в аргумент команды \fbox не получится, поскольку наш текст в одну строку не укладывается, а команда \fbox, подобно команде \mbox, текстов, не укладывающихся в строку, не переваривает. Поэтому нужно сделать из нашего абзаца блок с помощью команды \parbox и этот блок (т.е. уже "букву") передать в качестве аргумента команде \fbox:
\fbox{% \parbox{6cm}{% Внутри TeX'овских блоков может ... ... друг в друга, как матрешки.}% }Обратите внимание на знаки процента, которыми заканчиваются первая и предпоследняя строки. Если бы их не было, то рамка отстояла бы от текста больше, чем надо, так как TeX решил бы, что аргумент команды \fbox имеет пробел до и после "буквы", созданной командой \parbox. См.лекцию 1 по поводу использования знака процента для удаления нежелательных пробелов.